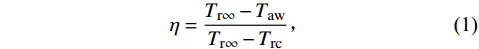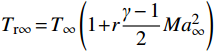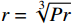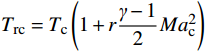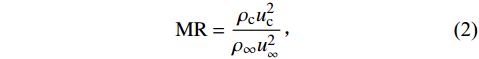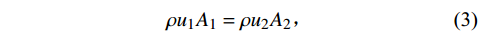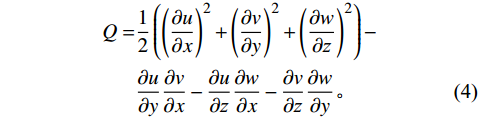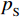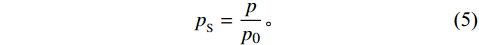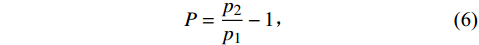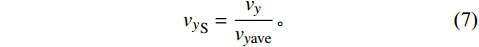Effect of mainstream Mach number on cooling flow field characteristics and cooling efficiency of supersonic air film
-
摘要:
着眼于离散孔形式的气膜冷却在高超声速飞行器热防护中的应用,为更深入探究超声速气膜冷却流场结构特征以及激波对气膜冷却的耦合作用机理,采用三维可压缩RANS数值仿真方法,研究了不同主流马赫数条件下气膜冷却的流动和传热特性。结果表明,主流超声速条件下,冷却射流的阻碍作用使得气膜冷却孔上游出现激波,且随着主流马赫数的增大,激波强度增大;激波诱导主流沿展向偏转而远离气膜冷却孔中心区域,弱化了主流和冷却射流的相互作用,降低了冷却射流在展向的掺混耗散。因此,在主流超声速条件下气膜冷却覆盖效果更佳、距离更长,且整体气膜冷却效率随着主流马赫数的增大而提高。
Abstract:With a view on the application of air film cooling in the form of discrete holes in hypersonic vehicle thermal protection, and in order to further understand the structural characteristics of supersonic air film cooling flow field and the coupling mechanism of shock waves on air film cooling, a 3D compressible RANS numerical simulation method was used to investigate the flow and heat transfer characteristics of air film cooling under different mainstream Mach numbers. The results show that, under mainstream supersonic conditions, the obstruction effect of the cooling jet causes shock waves to appear upstream of air film cooling holes, and the intensity of shock waves increases with the increase of mainstream Mach numbers. The shock wave induces the mainstream to deflect along the spanwise direction and move away from the central region of the air film cooling hole. Thus, the interaction between the mainstream and the cooling jet is weakened, and the mixing and dissipating strength of the cooling jet in the spanwise direction is reduced. Therefore, the coverage effect is better and the distance is longer for the air film cooling under supersonic mainstream conditions. In addition, the overall air film cooling efficiency increases with the increase of the mainstream Mach numbers.
-
0. 引言
热防护技术是超声速飞行器研制的关键技术之一。在多种主动热防护手段中,气膜冷却具有结构简单、冷却效果好的特点,在一定条件下还具有减阻效果[1],故而在超声速飞行器表面热防护方面展现出良好的应用潜力。气膜冷却自概念提出以来,就以其良好的冷却效果在航空发动机及燃气轮机涡轮叶片的冷却设计中得到较多应用[2]。科研人员对亚声速主流条件下的气膜冷却进行了细致的探究[3]。然而,针对超声速主流条件下的气膜冷却的研究相对较少。Goldstein等[4]通过实验研究了平板二维切向槽缝超声速气膜冷却,以吹风比和无量纲距离为自变量,拟合得到冷却效率关联式,研究发现超声速气膜冷却效果要好于亚声速气膜冷却。O’Conner等[5]在Goldstein实验的基础上进行了超声速气膜冷却的数值仿真研究,并对冷却效率关联式进行了修正。Cary等[6]的实验研究表明:由于超声速来流的速度更快,使冷却气体能够覆盖更长的距离;从切向槽缝喷出的冷却气体能有效减小下游壁面的表面阻力。
冷却射流与主流掺混过程中所形成的流场结构对下游气膜冷却的覆盖效果有重要影响。Konopka等[7]采用大涡模拟研究了超燃冲压发动机燃烧室的超声速气膜冷却,发现湍流注入会强化主/冷射流的掺混,进而降低气膜冷却效率。在探讨激波发生器诱发的激波对超声速气膜冷却效率影响方面,实验结果显示,激波作用区域的气膜冷却效率会降低,这主要是由于作用区域边界层的分离及边界层内流体速度下降[8-9]所致。数值仿真研究发现,外部激波降低了边界层流体的马赫数,导致绝热壁面温度升高;同时,激波作用诱发的涡结构会增强主流与冷却射流的掺混,使得冷却效率降低,且降低程度随着激波强度增加而增大[10-12]。为削弱激波对超声速气膜冷却的影响,有研究针对冷却介质流动特性进行数值仿真,结果表明:降低冷却介质温度和增加介质流动速度都能有效抑制激波作用处主/冷射流的掺混[13-14],提高气膜冷却效率。Marquardt等[15]数值分析了以氢气和氦气为冷却介质的超声速气膜冷却受外部激波的影响,结果显示氢气具有更高的气膜冷却效率。Peng等[16]从结构优化角度数值探究了带空腔的开槽壁在受激波作用的超声速气膜冷却中的应用,发现这种结构能有效弱化激波作用的影响。
上述超声速气膜冷却研究大多基于二维槽缝平板气膜冷却进行,且主要关注外部激波对气膜冷却的影响。近年来,随着气膜冷却在高超声速飞行器热防护中的应用,科研人员逐渐关注离散孔形式的超声速气膜冷却流动传热特性。Wittig等[17]通过实验和数值仿真探究气膜孔形状和角度对跨声速气膜冷却的影响,结果发现主流马赫数达1.2时,气膜孔上游出现激波,且激波强度和位置受气膜孔形状的影响。Ligrani等[18]实验研究了激波对平板气膜冷却的影响,发现当气膜孔上游存在激波时,气膜冷却效率相对更高。Zhang C X等[19]数值研究了激波对翼型表面气膜冷却的影响,得到了与Ligrani等实验研究相同的结论。Zhang B等[20]的数值研究进一步显示,激波会诱发逆压力梯度并导致局部气膜冷却效率降低。孙冰等[21]针对离散孔结构超声速气膜冷却进行数值探究,发现气膜孔入口收敛段剧烈收缩会降低流量系数从而弱化气膜冷却效果。罗晓波等[22]基于离散气膜孔数值探究晶格阵列结构对超声速气膜冷却的影响,发现晶格阵列结构的扰流作用使得展向气膜覆盖效果更佳。李俊等[23]数值探究入射角对超声速气膜冷却的影响,发现随着入射角的增大肾形涡强度增大,继而强化了主/冷射流的掺混,加剧了耗散,导致气膜冷却效率下降。陈四杰等[24]数值探究气膜孔位置对弱化激波作用的效果,发现气膜孔位于激波入射位置前缘能有效弱化激波对边界层的影响,而气膜孔位于激波入射位置下游对激波作用无任何影响。向纪鑫等[25]数值探究入射激波强度对超声速气膜冷却的影响,发现激波的引入在边界层诱发形成分离回流区,且分离回流区较小时,其高流阻促使冷却射流沿展向流动从而强化展向气膜覆盖;随着激波强度增大,分离回流区增大从而阻碍冷却射流向下游流动,继而强化主/冷射流的掺混,降低气膜冷却效率。然而,目前仍缺乏对激波的形成、形态、分布和发展等的分析,以及激波对冷却气体的出流和主/冷射流掺混影响的深入理解。
为进一步认识激波和气膜冷却耦合作用机理,以及超声速气膜冷却流场结构特征,本文采用数值计算方法,探究不同主流马赫数条件下超声速气膜冷却的流动和传热特性,尤其是气膜孔上游的激波对气膜冷却效率及主/冷射流掺混的影响机理,以期为超声速飞行器表面热防护设计提供参考。
1. 计算模型
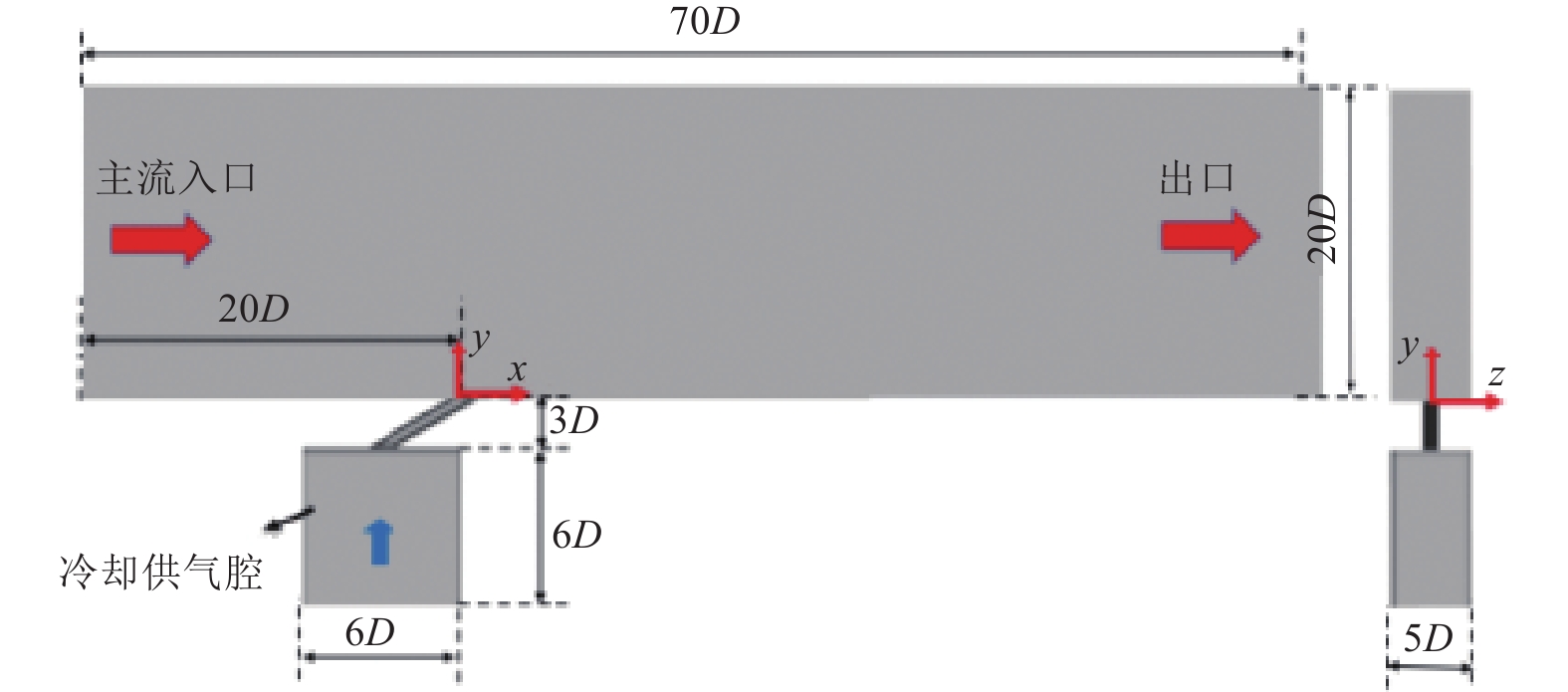
参考Ligrani等[18]的实验模型及倪航等[26]的数值模型,本研究的物理模型由主流通道、单气膜冷却孔(气膜孔)和冷却供气腔组成。其中,气膜孔射流角度α为30°,复合角为0°;气膜孔长径比L/D为6,展向间距P/D为5;为了降低气膜孔内流动不稳定性的影响,孔径D为2 mm。数值计算几何模型如图1所示:几何坐标原点为气膜孔出口中心,主流通道截面为20D×5D,主流入口截面与气膜孔的距离为20D,出口截面延伸至气膜孔下游50D处。为降低计算成本,主流流域两侧采用周期性边界条件,以简化气膜孔在展向方向的周期性排列。
2. 数值方法及验证
本文采用三维可压缩RANS有限体积法求解定常N-S方程,数值计算基于ANSYS CFX商业软件开展。在超声速主流工况下,强烈的气动加热使得流体温度急剧升高,进而引起流体的热传导系数和动力黏度发生变化。为准确模拟这一过程,本文依据Surtherland公式,对整个流域流体的动力黏度和热传导系数进行计算;同时,采用二阶迎风格式进行离散化处理,并选用SST k-ω湍流模型来更精确地描述流体动力学行为。
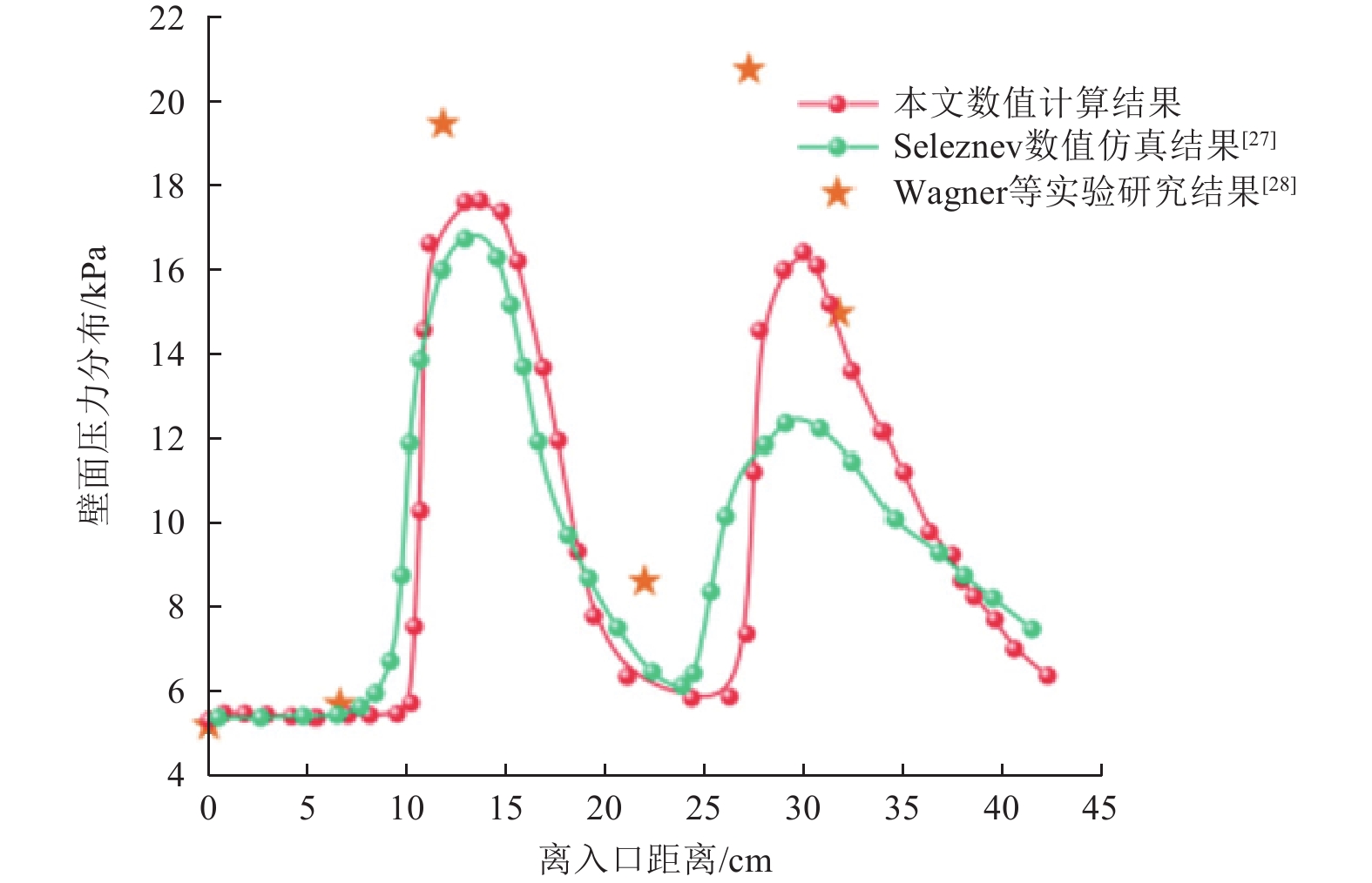
为验证数值计算方法的有效性,首先针对入口段包含一个6°压缩面的超燃冲压发动机进气道的超声速流动进行数值验证,通过壁面压力的沿程分布反映在激波作用下的流动特性变化,并将数值计算结果与Seleznev的数值仿真[27]和Wagner等的超声速流动实验研究[28]结果进行对比,如图2所示。可以看到,本文数值计算结果与上述2项研究结果的整体分布趋势基本一致,仅在反射激波作用处存在最大16%的偏差。
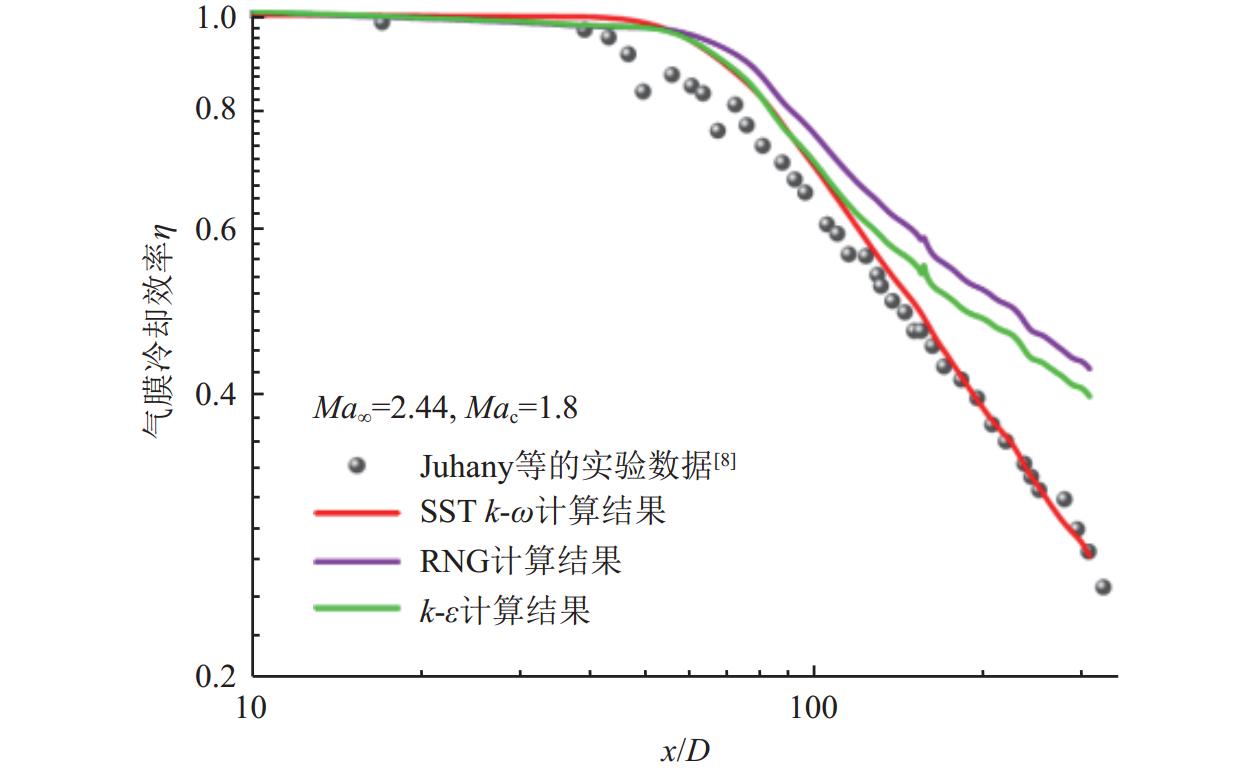
进一步针对主流马赫数Ma∞=2.44、冷气射流马赫数Mac=1.8工况下的二维切向槽缝气膜冷却进行数值验证。在本文研究中,采用气膜冷却效率η来衡量气膜冷却的覆盖效果,其定义为
$$ \eta = \frac{{{T_{{\mathrm{r}}\infty }} - {T_{\mathrm{aw}}}}}{{{T_{{\mathrm{r}}\infty }} - {T_{\mathrm{rc}}}}} \text{,} $$ (1) 式中:Tr∞为主流恢复温度,
$ {T_{{\mathrm{r}}\infty }} = {T_\infty }\left( {1 + r\dfrac{{{\textit{γ}} - 1}}{2}M{a_\infty ^2}} \right)$ ,其中,r为恢复系数($ r = \sqrt[3]{Pr} $ ),γ为流体的比热比;Trc为冷却射流恢复温度,$ {T_{{\mathrm{rc}}}} = {T_{\mathrm{c}}}\left( {1 + r\dfrac{{{\textit{γ}} - 1}}{2}M{a_{\mathrm{c}}^2}} \right) $ ;Taw为绝热壁面温度。用3种湍流模型(k-ε, RNG和SST k-ω)计算的结果对比Juhany等的实验数据[8],如图3所示。可以看到,SST k-ω湍流模型的数值计算结果同实验结果的吻合度最高,最大偏差小于11%。
上述验证表明,本文采用的数值计算方法和计算模型精度较高,能够满足本文研究的需要。
3. 网格及网格无关性验证
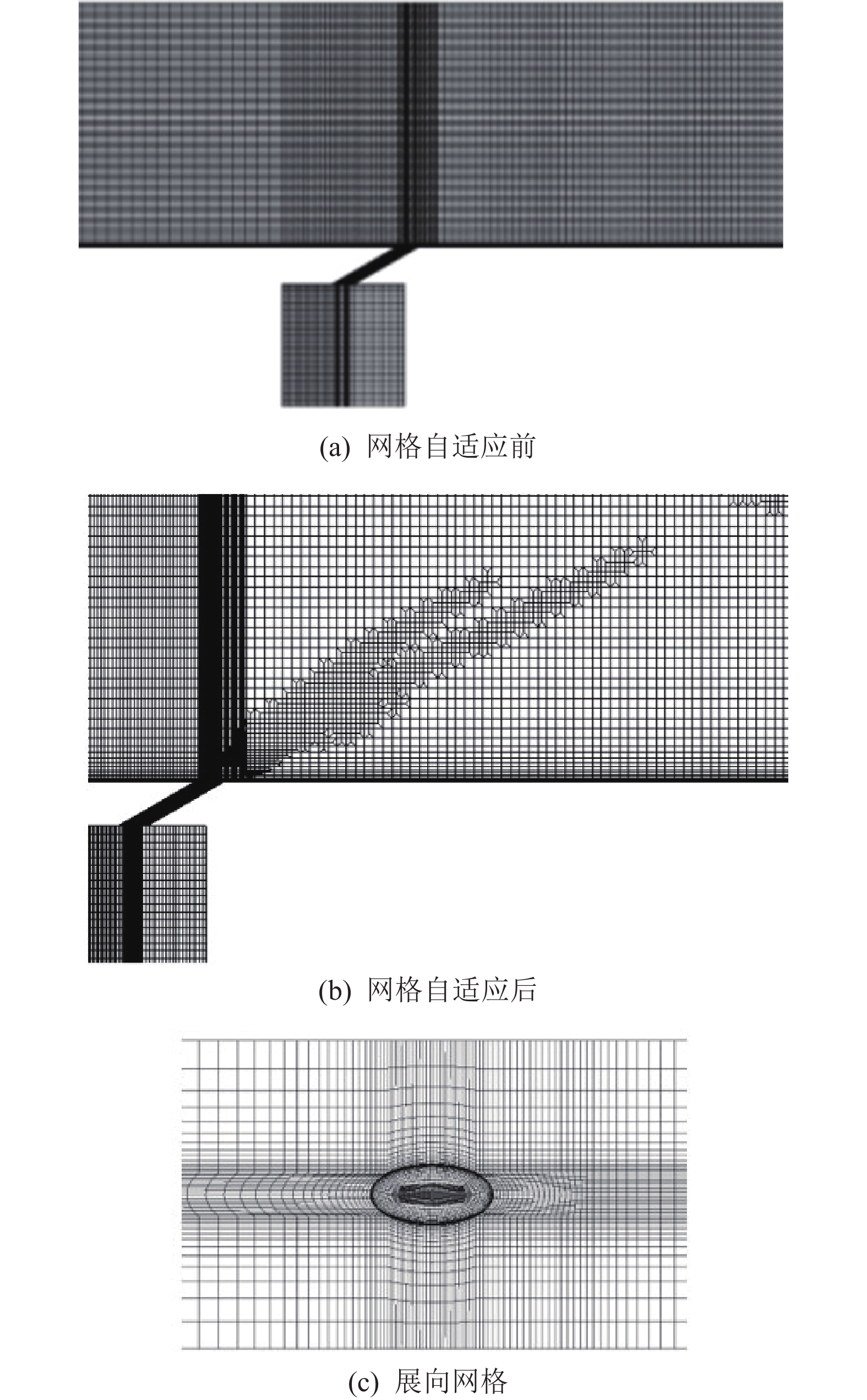
本文计算采用结构化网格(如图4所示),对气膜孔附近及壁面流动边界层区域进行了网格加密,使得第1层网格的无量纲壁面距离y+≤1,从而满足湍流模型计算条件。
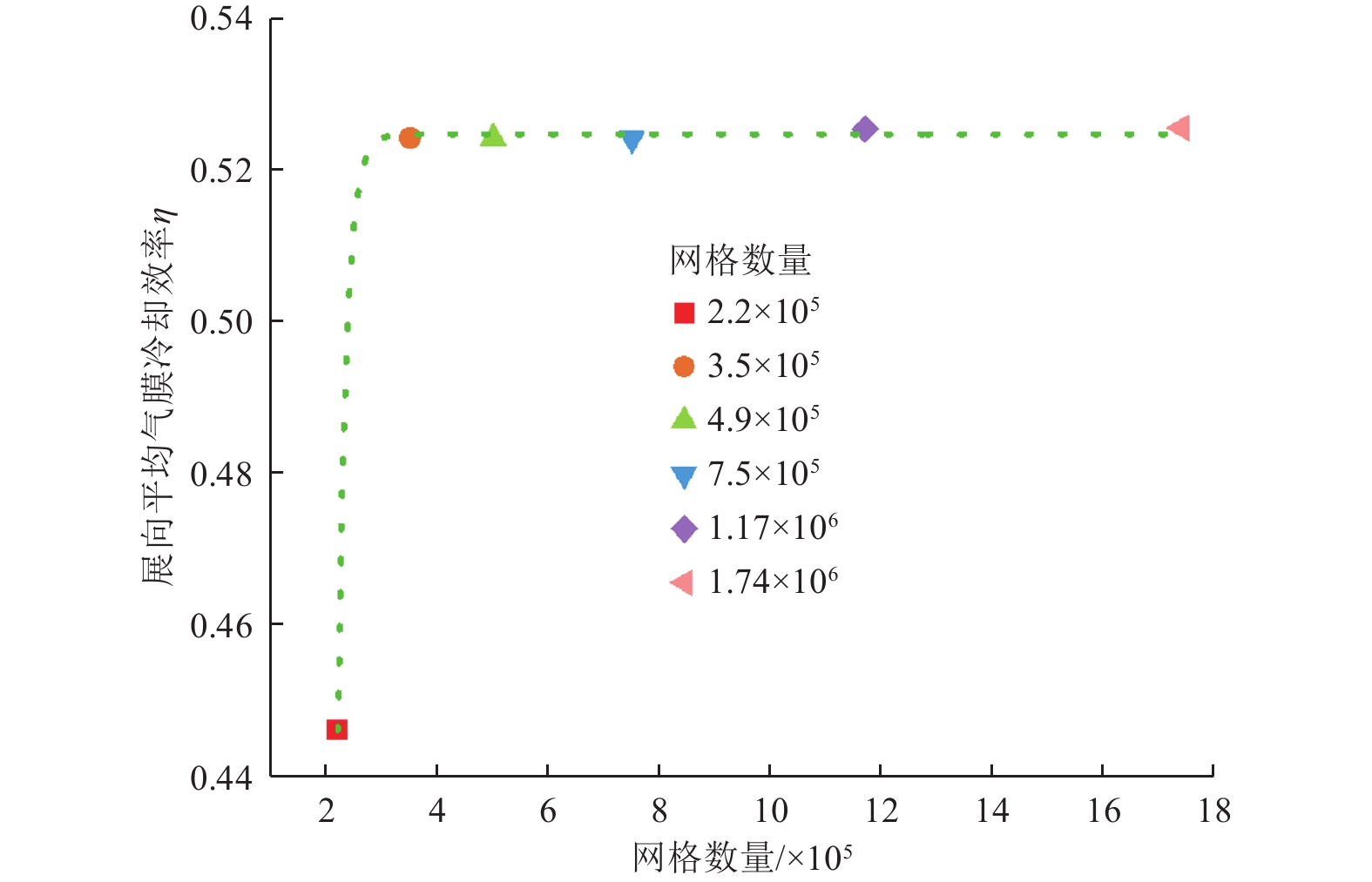
针对物理模型进行网格无关性验证。在Ma∞=2工况条件下,分别选用数量为2.2×105、3.5×105、4.9×105、7.5×105、1.17×106和1.74×106的网格。考虑到超声速主流工况下流场结构的复杂性,为了精确捕捉激波,基于压力梯度自适应网格法对激波作用位置进行局部加密。不同网格计算获得的平均气膜冷却效率如图5所示。
可以看到,当网格数超过3.5×105后,不同网格计算的平均气膜冷却效率趋于一致,整体变化较小。因此,本文将计算网格数量控制在3.5×105左右,网格自适应后的网格数为5.33×105左右。
4. 边界条件
主流入口和冷却射流入口均设置为速度入口边界条件,出口为压力出口,上边界为开放边界条件,其余壁面为无滑移绝热壁面。本文所研究的是气膜冷却在高超声速飞行器表面热防护中的应用,故主流介质选取为空气,其温度和压力参数以30 km高空大气环境为参照。为了减小燃烧和化学反应等因素的潜在影响,同时为保证后续实验探究安全可靠地开展,本文选用化学性质相对稳定的氮气(N2)作为冷却介质。为探究不同主流马赫数对流场结构及气膜冷却效率的影响,共计算了3种工况,主流及冷却射流的边界条件详见表1。出口静压设定为1197 Pa,冷却射流与主流的动量比为MR=0.1。
表 1 计算边界条件Table 1. Computational boundary conditions主流边界条件 入口速度u∞/(m·s-1) 241 604 1 207.25 马赫数Ma∞ 0.8 2 4 入口静温T∞/K 226.51 冷却射流边界条件 入口速度uc/(m·s-1) 82 127.32 254.65 马赫数Mac — 入口静温Tc/K 200 冷却射流与主流的动量比MR的定义为
$$ {\mathrm{MR}} = \frac{{{\rho _{\mathrm{c}}}u_{\mathrm{c}}^2}}{{{\rho _\infty }u_{_\infty }^2}} \text{,} $$ (2) 式中:uc和ρc分别为气膜孔出口冷却射流的平均流速和平均密度;u∞和ρ∞分别为主流入口的平均流速和平均密度。
表1给出的冷却射流入口速度为气膜孔出口y方向平均速度分量。根据质量守恒定律,有
$$ \rho {u_1}{A_1} = \rho {u_2}{A_2} \text{,} $$ (3) 式中:u1和u2分别为供气腔进气速度和气膜孔出口y方向平均速度;A1和A2分别为供气腔入口面积和气膜孔出口面积;ρ为冷却气体的密度。
5. 结果与讨论
5.1 主流马赫数对射流流场结构的影响
在分析主流马赫数对流场结构的影响时,保持冷却射流与主流的动量比MR=0.1。为表征流场结构的变化情况,基于Q准则对涡的位置和形状进行可视化,Q准则定义式为
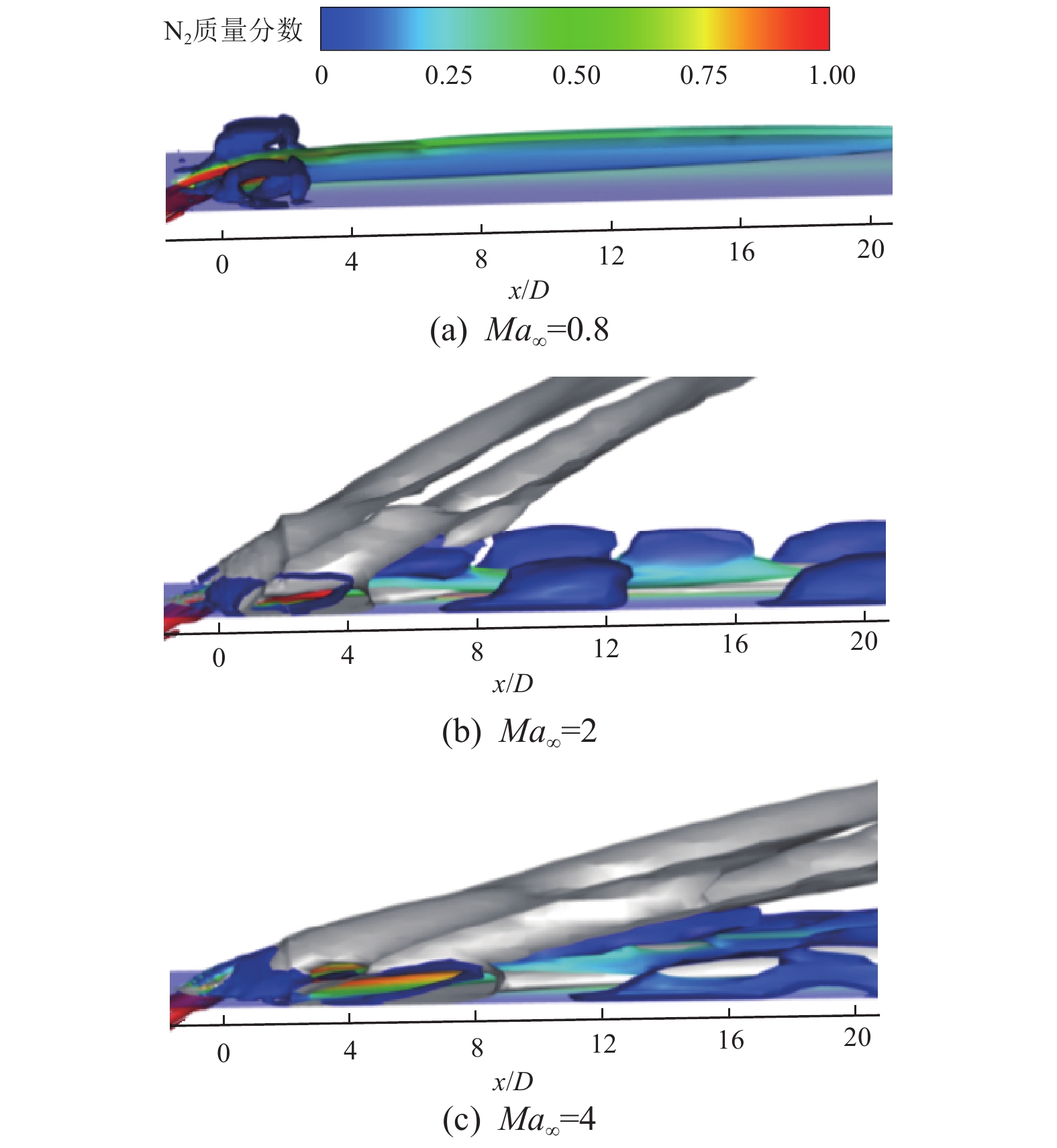
$$\begin{split} Q = & \frac{1}{2}\left( {{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial {\textit{z}}}}} \right)}^2}} \right) -\\ & \frac{{\partial u}}{{\partial y}}\frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial {\textit{z}}}}\frac{{\partial w}}{{\partial x}} - \frac{{\partial v}}{{\partial {\textit{z}}}}\frac{{\partial w}}{{\partial y}} 。\end{split} $$ (4) 图6所示为Q=0.01并映射有N2质量分数的气膜孔出口流场结构等值面,激波由速度梯度显示出的灰色结构表示。在Ma∞=2和Ma∞=4工况下,在气膜孔前缘观察到斜激波的形成;斜激波沿主流方向从靠近气膜孔上游位置以一定角度斜向上传播,其传播方向随主流马赫数的增大逐渐靠近冷却壁面。冷却射流的流向在主流持续切向力的作用下向主流方向偏转,在偏转处出现膨胀激波(从图6中可以观察到气膜孔后缘附近膨胀激波的出现)。主流和冷却射流的相互作用在气膜孔出口形成肾形涡,而肾形涡因其旋流特性使得主流被卷夹从而同冷却射流进行掺混;随着射流核心沿流向发展,冷却射流逐渐耗散,其质量分数也相应降低。总之,由于激波的作用,展向两侧的流动特性变得复杂,可以观察到复杂的涡结构,这种涡系的存在对射流主体的发展具有一定影响。
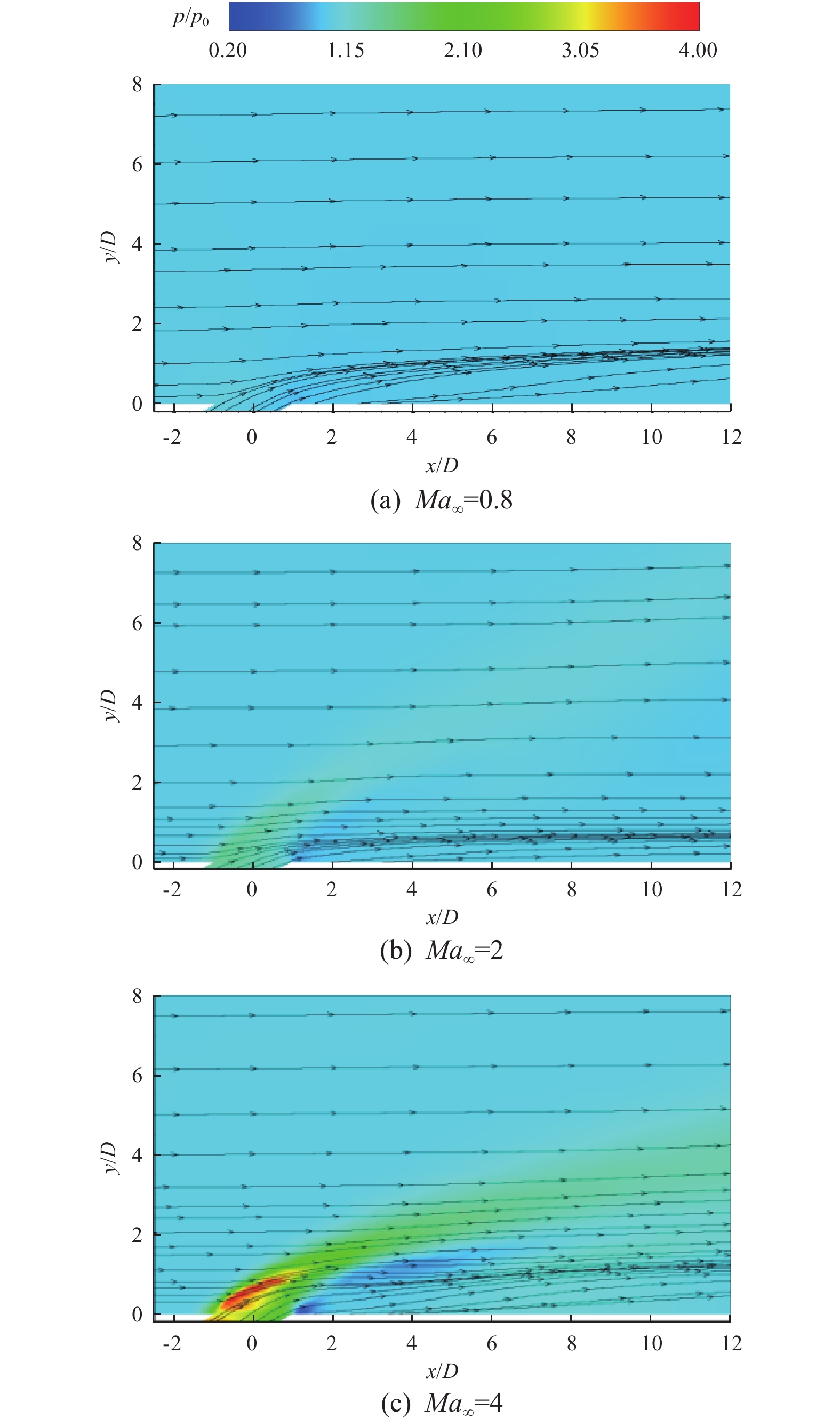
为具体分析不同主流马赫数条件下的流场结构差异,引入无量纲压力
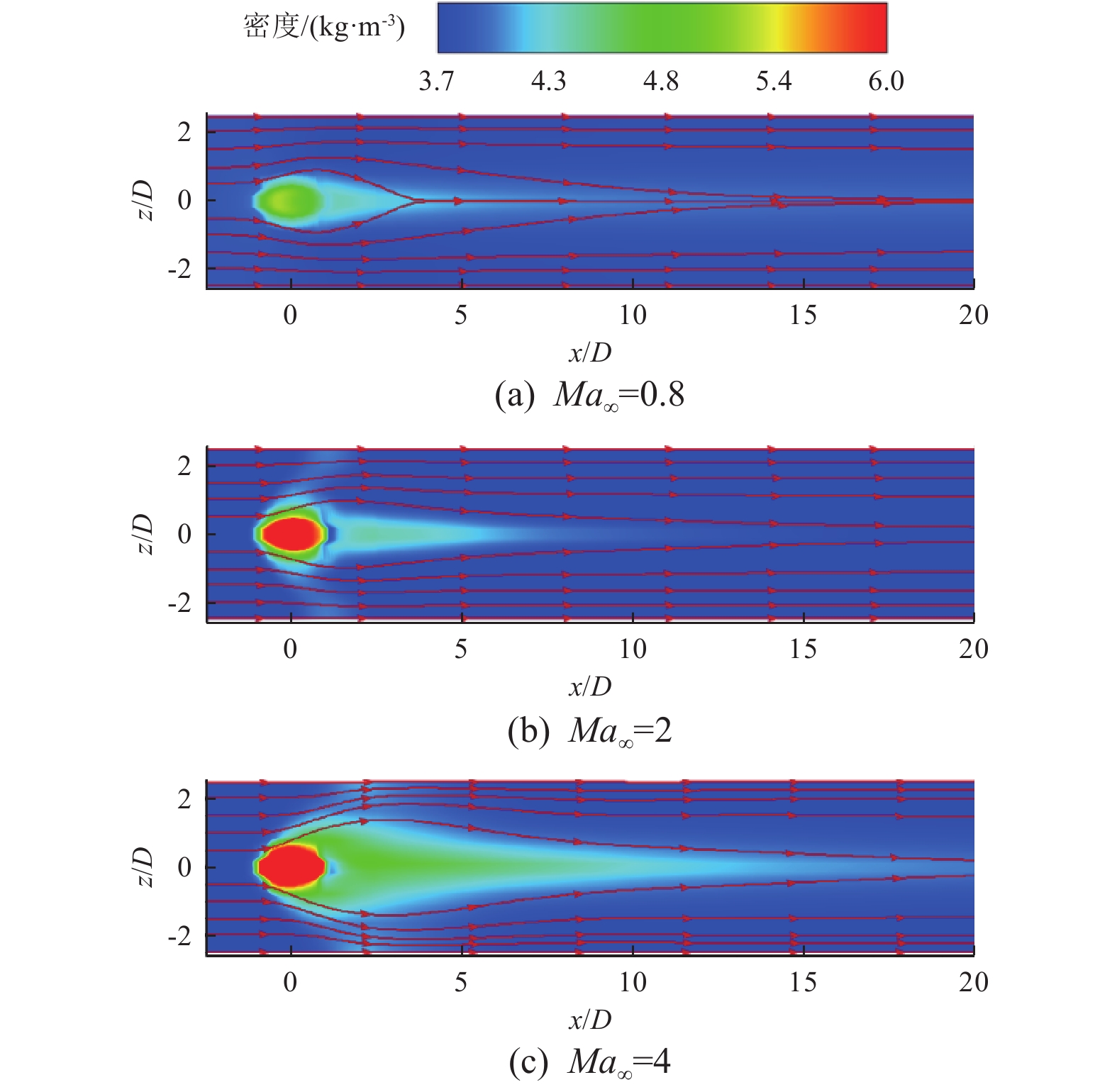
$p_{_{\mathrm{S}}} $ ,其定义为当地压力p同主流入口压力p0的比值,$$ p_{_{\mathrm{S}}}=\frac{p}{p_0} {。}$$ (5) 图7为不同主流马赫数条件下对称截面的无量纲压力分布云图和流线图。可以看出:Ma∞=0.8工况下,整体压力分布较为均匀;然而,在Ma∞=2和Ma∞=4工况下,由于斜激波的作用,可以明显观察到气膜孔出口区域存在局部高压区,且局部高压区的压力值随着主流马赫数的增大而明显增大。
激波强度的定义为
$$ P = \frac{{{p_2}}}{{{p_1}}} - 1 \text{,} $$ (6) 式中,p1和p2分别为激波前、后的压力。可见,气膜孔上游的斜激波强度将随主流马赫数的增大而增大。
从图7中的流线图可以观察到,冷却射流迎风侧的流线在主流持续横向切向力的作用下逐渐趋于主流流向,同时冷却射流对主流流动也形成一定的阻碍,迫使主流的流向发生改变:在Ma∞=0.8工况下,主流流向的偏折只出现在气膜孔附近;而在Ma∞=2和Ma∞=4工况下,由于斜激波的作用,除了气膜孔附近,在远离壁面区域的主流也发生了流向偏转,且偏转程度随着激波强度的增大而增大。
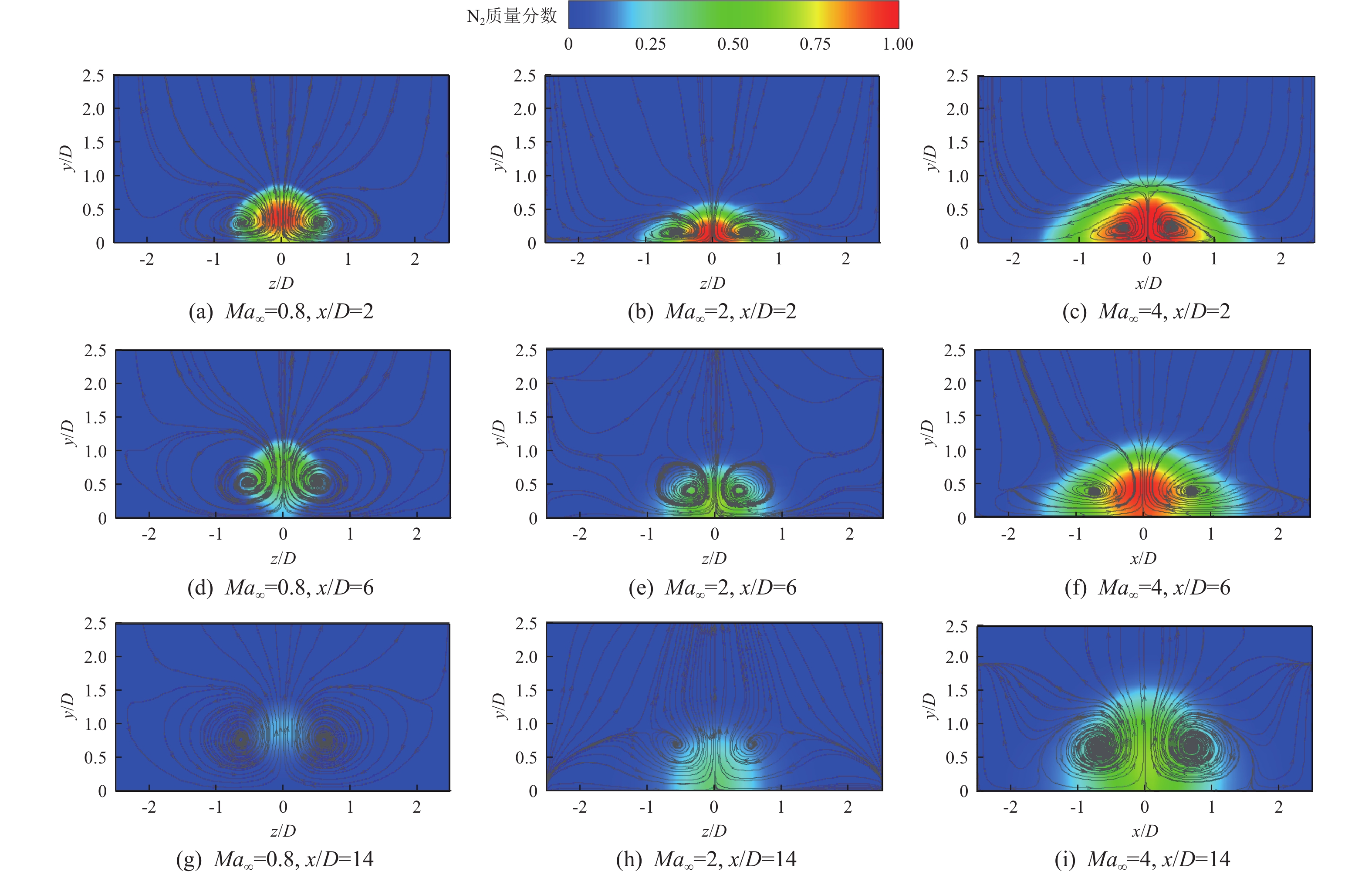
图8为不同主流工况下气膜孔下游2D、6D和14D处流向截面的N2质量分数分布云图与流线图。通过N2质量分数分布云图可以观察到,沿着主流流动方向,冷却射流质量分数逐渐降低。分析主要是由于周围的高温主流不断被卷吸而与冷却射流掺混,使得冷却气体不断耗散,原本扁平状的冷却射流也逐渐扩散;随着扩散程度的加深,冷却射流体积膨胀,同主流接触面积增大,会进一步加剧两种气体的掺混,直至冷却射流同主流完全掺混消失,其对壁面的冷却效果随之逐渐降低。同时,由于肾形涡的旋转,涡对中心存在y方向的速度分量,致使冷却射流在流动过程中不断被推离壁面,同壁面的接触面积持续减小,这进一步加剧了壁面展向气膜覆盖范围向中心区域的收缩趋势。
通过各流向截面上N2质量分数分布云图还可以观察到:相较于Ma∞=0.8工况,Ma∞=2和Ma∞=4工况下高质量分数的冷却射流主要集中在近壁区域,且近壁区域高质量分数的展向宽度随着主流马赫数的增大而增大;同时,冷却气体的耗散在Ma∞=2和Ma∞=4工况下明显低于Ma∞=0.8工况下的,且随着主流马赫数的增大,其耗散程度逐渐降低。
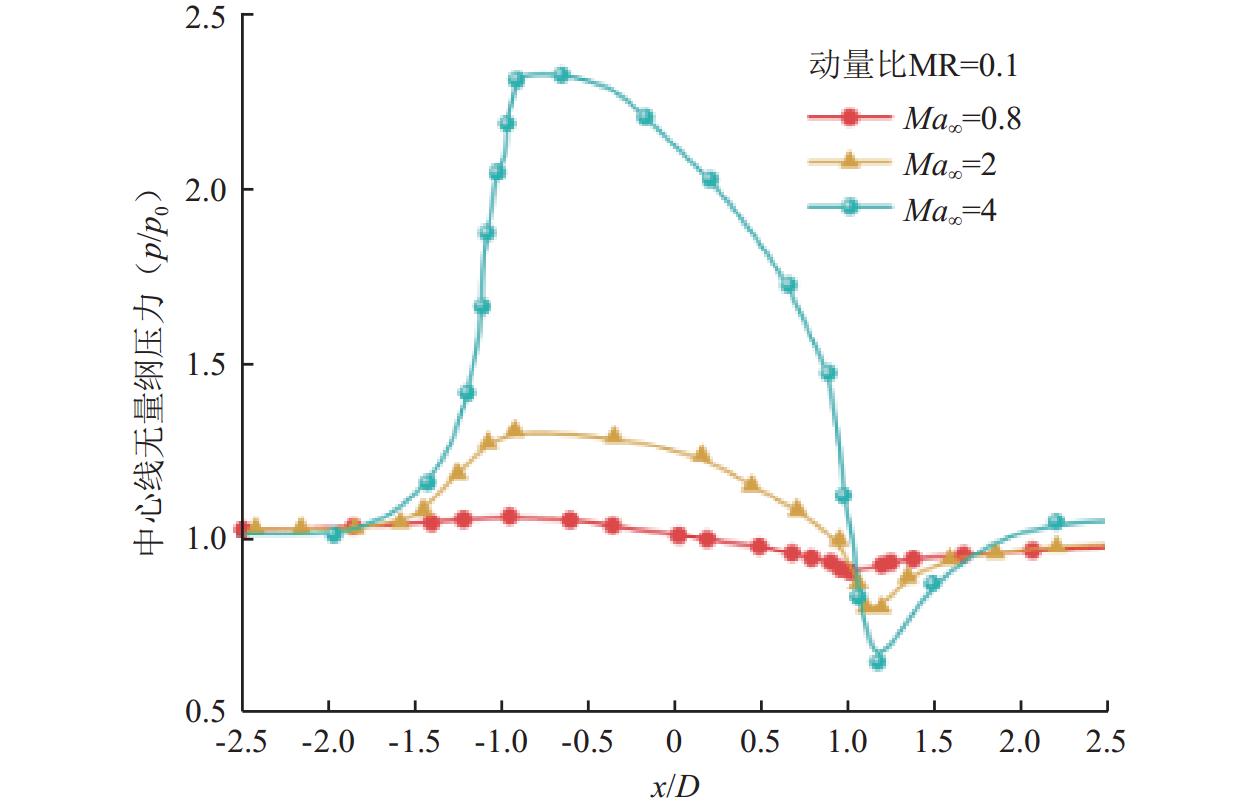
图9为冷却壁面中心线无量纲压力分布,横轴显示范围从x/D=-2.5到x/D=2.5。从图中可以观察到:在Ma∞=0.8工况下,无量纲压力分布呈现出相对平稳的态势,压力峰值为1.05;而在Ma∞=2和Ma∞=4工况下,受激波的作用,在气膜孔上游位置压力开始显著增大。Ma∞=2时,压力在x/D=-1.6位置开始增大,压力峰值为1.28;Ma∞=4时,压力从x/D=-1.9位置就开始增大,压力峰值达到2.38。可见,随着主流马赫数的增大,主流和冷却射流的相互作用增强,气膜孔出口的压力分布出现剧烈波动,超声速工况下的压力波动幅值远大于亚声速工况下的,并且Ma∞=4工况下的压力波动最大。
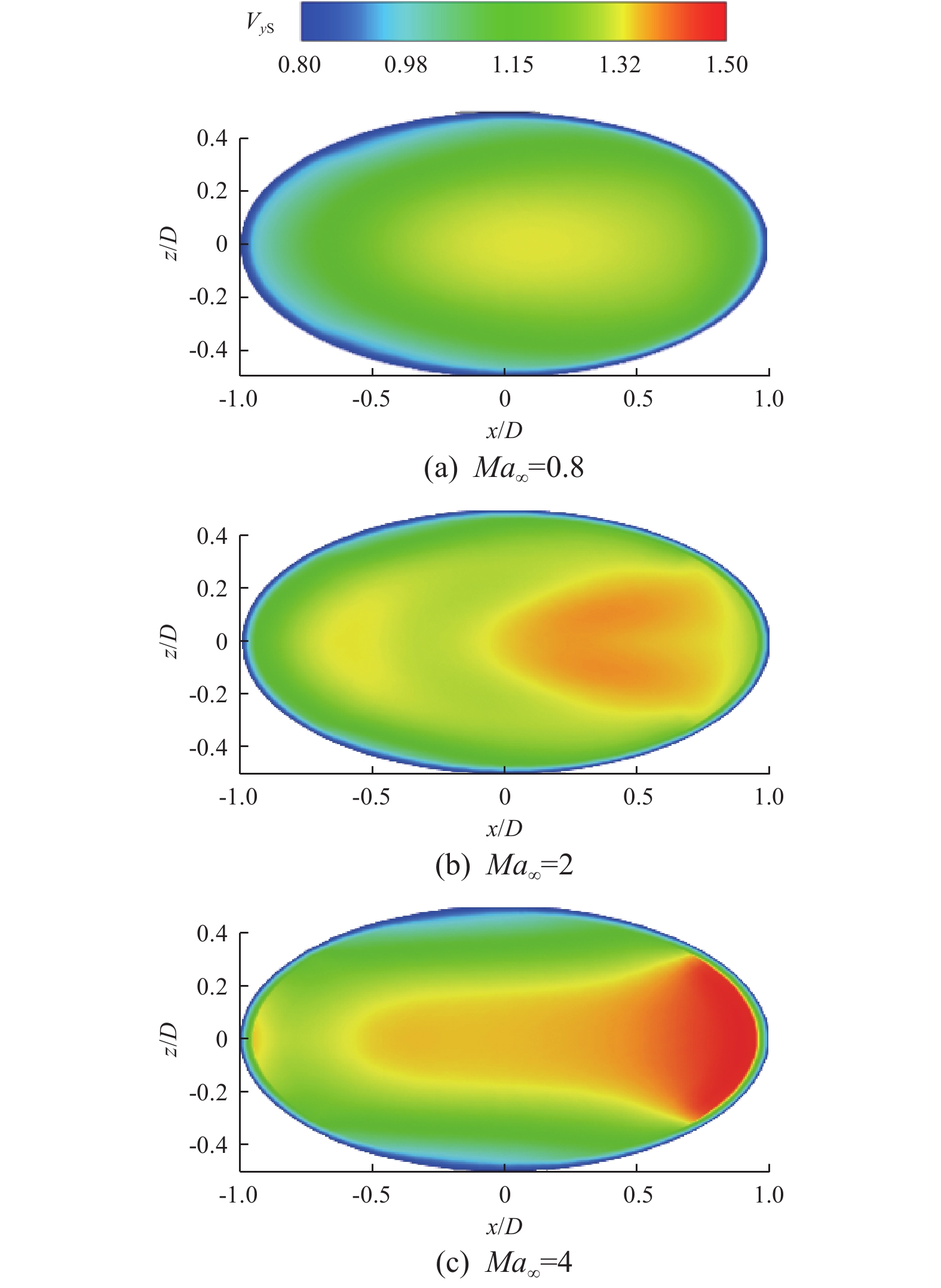
气膜孔出口处不均匀的压力分布形成不均匀的冷却射流速度分布。为具体分析不同主流马赫数条件下的气膜孔出口速度分布,引入无量纲速度vyS,其定义为当地y方向速度分量vy同y方向平均速度分量vyave的比值,即
$$ {v_y}_{\mathrm{S}} = \frac{{{v_y}}}{{{v_{y{\mathrm{ave}}}}}} 。 $$ (7) 图10为气膜孔出口冷却射流y方向无量纲速度分布云图,可以看到:在Ma∞=0.8工况下,速度分布整体上较为均匀;在Ma∞=2和Ma∞=4工况下,受气膜孔出口压力分布不均匀的影响,在气膜孔下游局部低压区域冷却射流y方向速度分量更大;而在上游的局部高压区冷却射流y方向速度分量则更小。分析可知,随着主流马赫数的增大,气膜孔上游形成的激波强度增大,加剧了气膜孔出口压力波动,使得气膜孔出口冷却射流速度分布不均匀的情况更为显著。这些因素使得冷却射流流出气膜孔后,迎风侧同主流进行掺混的冷却气体质量分数相对更小,而背风侧对冷却壁面进行气膜覆盖的冷却气体质量分数相对更大。这种分布有利于降低冷却射流同主流掺混引起的耗散,提升下游气膜冷却的覆盖效率。
图11所示为y/D=0.5水平截面的密度分布云图和流线图。激波的强压缩性使穿过的主流密度增大,从密度云图可以观察到,在超声速主流Ma∞=2和Ma∞=4工况下,激波的出现导致展向两侧主流密度增大。结合流线图可以看出,相较于气膜孔上游无激波的Ma∞=0.8工况,在Ma∞=2和Ma∞=4工况下,气膜孔上游的斜激波诱使主流向远离冷却射流主体的展向偏转,从而弱化了主流和冷却射流的相互作用。随着沿流向的发展,展向两侧的主流气体在冷却射流卷吸作用下逐渐重新汇聚于气膜孔中心区域;且由于主流流向的偏转,冷却射流卷吸对主流的影响明显更弱,主流向中心区域汇聚的流线更少,汇聚程度降低。相较于Ma∞=2工况,Ma∞=4工况下的激波强度更大,使主流沿展向偏转的程度更深,故Ma∞=4工况下主流和冷却射流展向相互作用最弱,冷却射流在展向区域的耗散最少,展向气膜覆盖效果最好。
5.2 气膜冷却效率对比分析
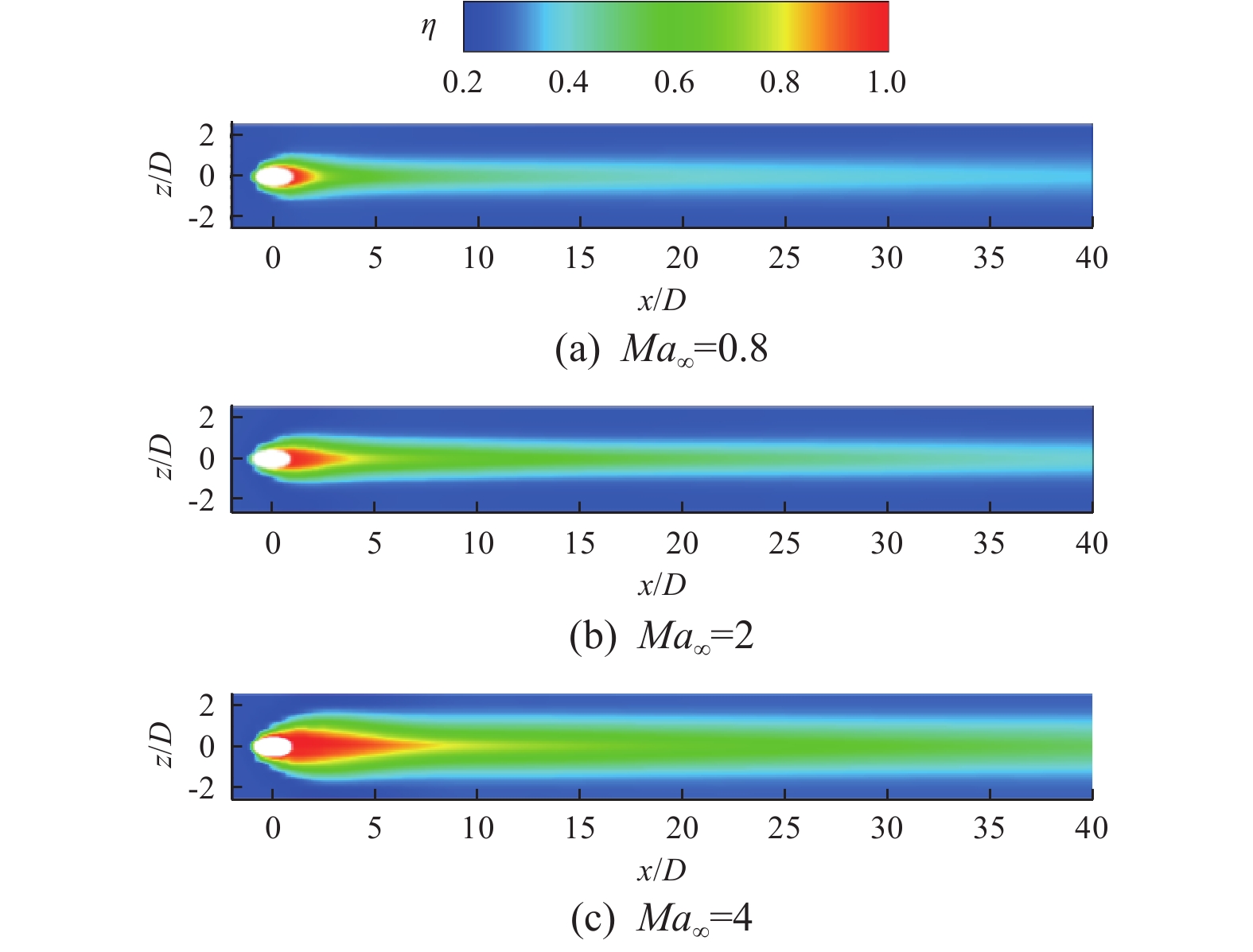
不同主流条件下,冷却射流与主流相互作用形成的流场结构存在明显差异。本节主要分析该流场结构特征,尤其是气膜孔上游激波对气膜冷却效果的影响。图12展示了Ma∞=0.8、Ma∞=2和Ma∞=4工况下的壁面气膜冷却效率分布云图。可以看到:气膜孔出口附近区域的冷却效率较高,且冷却壁面中心区域的高于展向区域的;随着冷却射流与主流的掺混及耗散,气膜冷却效率顺主流方向逐渐降低,展向气膜覆盖范围逐渐向中心区域收缩;Ma∞=2和Ma∞=4工况下的气膜冷却效率整体上比Ma∞=0.8工况下的明显更高,其展向冷却效率分布更均匀,并且射流尾迹在下游保持更长的有效覆盖距离。
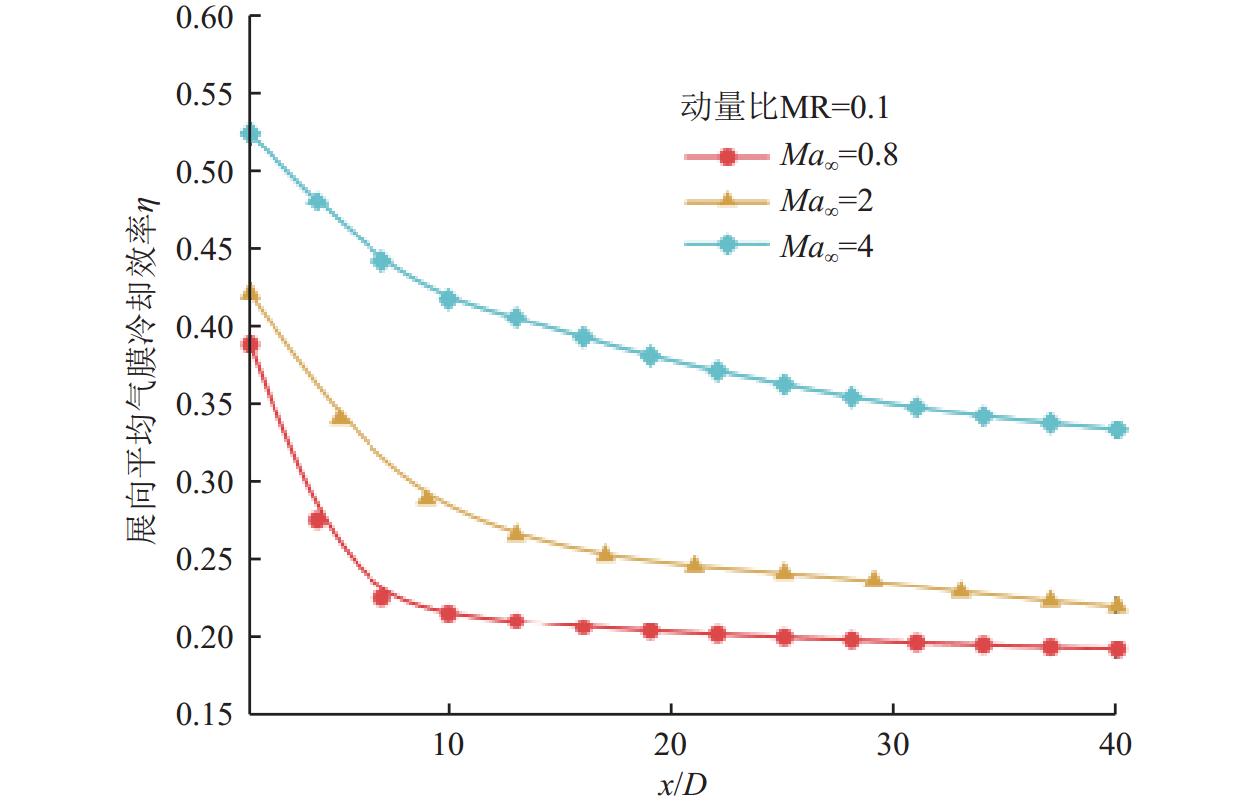
图13所示为展向平均气膜冷却效率的比较,可以看出,3种工况条件下的展向平均气膜冷却效率均随着冷却射流与主流的掺混和耗散而趋于降低,但沿着主流方向总体变化较为平缓;Ma∞=2和Ma∞=4工况下的展向平均气膜冷却效率整体较Ma∞=0.8工况下的更高,其中Ma∞=4工况下的展向平均气膜冷却效率最高,在下游区域依然能维持在0.35以上。
6. 结论
本文采用数值方法对超声速主流条件下主流与冷却射流相互作用形成的流场结构以及气膜冷却效率分布进行研究,分析了主流马赫数条件对流场结构及气膜冷却效率的影响机理,得到如下主要结论:
1)超声速主流条件下,冷却射流的出流对主流的阻碍使得气膜孔上游形成激波;随着主流马赫数的增大,激波位置向上游移动,强度增大,波后压力峰值增大。
2)在相同的冷却射流与主流动量比条件下,超声速主流下的气膜冷却效率较亚声速主流下的更高,有效气膜覆盖距离能保持得更长,即气膜冷却效率随着主流马赫数的增大而增大。
3)超声速主流条件下,激波诱导主流流向沿展向远离射流中心偏转,减弱了展向两侧主流和冷却射流的相互掺混作用,使冷却射流在展向区域的掺混耗散更小,因而展向气膜覆盖效果更好,整体冷却性能更佳。
4)超声速主流条件下,激波增大了气膜孔出口压力分布的不均匀程度,且这种不均匀程度随着主流马赫数的增大而加剧。这使得气膜孔出口迎风侧与主流进行掺混的冷却射流的质量分数相对更小,而背风侧对冷却壁面进行气膜覆盖的冷却射流的质量分数相对更大,相当于降低了冷却射流的掺混耗散,从而表现出更好的展向气膜覆盖效果。
以上结论对优化超声速飞行器表面热防护设计具有指导意义。
-
表 1 计算边界条件
Table 1 Computational boundary conditions
主流边界条件 入口速度u∞/(m·s-1) 241 604 1 207.25 马赫数Ma∞ 0.8 2 4 入口静温T∞/K 226.51 冷却射流边界条件 入口速度uc/(m·s-1) 82 127.32 254.65 马赫数Mac — 入口静温Tc/K 200 -
[1] PUDSEY A S, BOYCE R R, WHEATLEY V. Hypersonic viscous drag reduction via multi-porthole injector arrays[J]. Journal of Propulsion & Power, 2013, 29(5): 1087-1096
[2] DANNENBERG R E. Helium film cooling on a hemisphere at a Mach number of 10: NASA TN D-1550[R], 1962
[3] ZHANG S L, LI X, ZUO J Y. Research progress on active thermal protection for hypersonic vehicles[J]. Progress in Aerospace Sciences, 2020, 119: 100646 DOI: 10.1016/j.paerosci.2020.100646
[4] GOLDSTEIN R J, ECKERT E R G, TSOU F, et al. Film cooling with air and helium injection through a rearward-facing slot into a supersonic air flow[J]. AIAA Journal, 1966, 4(6): 981-985 DOI: 10.2514/3.3591
[5] O’CONNER J P, HAJI S A. Numerical study of film cooling in supersonic flow[J]. AIAA Journal, 1992, 30(10): 2426-2433 DOI: 10.2514/3.11243
[6] CARY A M JR, HEFNER J N. Film-cooling effectiveness and skin friction in hypersonic turbulent flows[J]. AIAA Journal, 1972, 10(9): 1188-1193 DOI: 10.2514/3.50348
[7] KONOPKA M, MEINKE M, SCHRODER W. Large-eddy simulation of supersonic film cooling at laminar and turbulent injection[C]//17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. San Francisco CA, USA, 2011
[8] JUHANY K A, HUNT M L, SIVO J M. Influence of injectant Mach number and temperature on supersonic film cooling[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(1): 59-67 DOI: 10.2514/3.501
[9] TAKESHI K, FUMIEI O, MASAHIRO T, et al. Experimental studies of supersonic film cooling with shock wave interaction[J]. AIAA Journal, 1996, 34(2): 265-271 DOI: 10.2514/3.13060
[10] PENG W, JIANG P X. Influence of shock waves on supersonic film cooling[J]. Journal of Spacecraft and Rockets, 2009, 46(1): 67-73 DOI: 10.2514/1.38458
[11] KONOPKA M, MEINKE M, SCHRÖDER W. Large-eddy simulation of high Mach number film cooling with shock-wave interaction[J]. Progress in Flight Physics, 2013, 5: 309-326
[12] SUN X K, NI H, ZHU Y H. Influence of shock wave impinging region on supersonic film cooling[J]. Chinese Journal of Aeronautics, 2021, 34(5): 452-465 DOI: 10.1016/j.cja.2020.12.012
[13] MARQUARDT P, KLAAS M, SCHRODER W. Comparison of shock/cooling-film interaction for cooled and isoenergetic injection[J]. AIAA Journal, 2020, 58(5): 2078-2092 DOI: 10.2514/1.J058471
[14] PENG W, SUN X K, JIANG P X. Effect of coolant inlet conditions on supersonic film cooling[J]. Journal of Spacecraft and Rockets, 2015, 52(5): 1456-1464 DOI: 10.2514/1.A33268
[15] MARQUARDT P, MEINKE M, SCHRODER W. Large-eddy simulation of shock-cooling-film interaction at helium and hydrogen injection[J]. Physics of Fluids, 2013, 25(10): 106101 DOI: 10.1063/1.4823745
[16] PENG W, JIANG P X. Effect of shock waves on supersonic film cooling with a slotted wall[J]. Applied Thermal Engineering, 2014, 62(1): 187-196 DOI: 10.1016/j.applthermaleng.2013.09.013
[17] WITTIG S, SCHULZ A, GRITSCH M, et al. Transonic film cooling investigations: effects of hole shapes and orientations[C]//International Gas Turbine and Aeroengine Congress and Exhibition. Birmingham: The American Society of Mechanical Engineers, 1996: 96-GT-222
[18] LIGRANI P M, SAUMWEBER C, SCHULZ A, et al. Shock wave-film cooling interactions in transonic flows[J]. Journal of Turbomachinery, 2001, 123(4): 788-797 DOI: 10.1115/1.1397305
[19] ZHANG C X, HASSAN I. Computational study of the effects of shock waves on film cooling effectiveness[J]. Journal of Engineering for Gas Turbines and Power, 2009, 131(3): 031901 DOI: 10.1115/1.3026568
[20] ZHANG B, HONG Q, LI J Q, et al. Effect of forward expansion angle on film cooling characteristics of shaped holes[J]. Thermal Science, 2020, 24(3B): 2279-2288
[21] 孙冰, 王太平, 张佳. 离散孔结构超声速气膜冷却数值模拟[J]. 航空动力学报, 2017, 32(12): 2927-2933 SUN B, WANG T P, ZHANG J. Numerical simulation of discrete holes supersonic gaseous film cooling[J]. Journal of Aerospace Power, 2017, 32(12): 2927-2933
[22] 罗晓波, 杨艳静, 杨泽楠, 等. 晶格阵列结构与主流高超声速气膜冷却交互作用的数值研究[J]. 航天器环境工程, 2021, 38(2): 115-121 DOI: 10.12126/see.2021.02.001 LUO X B, YANG Y J, YANG Z N, et al. Numerical study of the interactions between lattice array structure and mainstream hypersonic film cooling[J]. Spacecraft Environment Engineering, 2021, 38(2): 115-121 DOI: 10.12126/see.2021.02.001
[23] 李俊, 张华良, 高阿飞, 等. 入射角对超声速平板气膜冷却的影响[J]. 汽轮机技术, 2023, 65(1): 1-5; 56 LI J, ZHANG H L, GAO A F, et al. Influence of incidence angle on supersonic film cooling of flat plate[J]. Turbine Technology, 2023, 65(1): 1-5
[24] 陈四杰, 单勇, 张靖周, 等. 涡轮叶栅超声速流场流动特征与气膜冷却特性[J]. 航空动力学报, 2013, 28(11): 2448-2454 CHEN S J, SHAN Y, ZHANG J Z, et al. Flow field and film cooling characteristics in supersonic turbine cascade[J]. Journal of Aerospace Power, 2013, 28(11): 2448-2454
[25] 向纪鑫, 李志强, 刘鹏, 等. 耦合传热下激波对超声速气膜冷却影响[J]. 航空动力学报, 2023, 38(2): 344-353 XIANG J X, LI Z Q, LIU P, et al. Effect of shock wave on supersonic film cooling under coupled heat transfer[J]. Journal of Aerospace Power, 2023, 38(2): 344-353
[26] NI H, WANG M, JIANG P X. A numerical study of segmented cooling-stream injection in supersonic film cooling[J]. Chinese Journal of Aeronautics, 2023, 36(6): 156-171
[27] SELEZNEV R K. Validation of two-dimensional model by the example of a supersonic inlet-isolator[J]. Journal of Physics, 2018, 1009: 012030
[28] WAGNER J L, YUCEIL K B, VALDIVIA A, et al. Experimental investigation of unstart in an inlet/isolator model in Mach 5 flow[J]. AIAA Journal, 2009, 47(6): 1528-1542 DOI: 10.2514/1.40966




 下载:
下载: