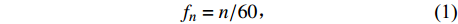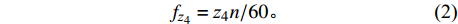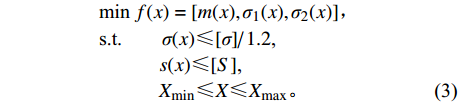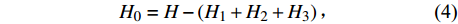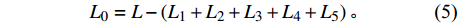0.   引言

近年来，在响应国家“双碳”目标落地推进的过程中，新能源产业得到飞速发展，新能源汽车的市场占有量愈来愈高。而结构轻量化技术是推进新能源汽车发展的关键技术之一，受到业界广泛关注。付强等^[1]基于铝合金材料的应用，用ABAQUS软件分析了车架的静强度性能，并通过分析结果反推车架的材料强度分布，实现了可满足各项指标要求的车架轻量化设计。周松等^[2]对整车部件进行位移、强度、模态和质量的灵敏度计算，定义相对灵敏度；并运用相对灵敏度分析的结果确定优化设计变量，在保证整车动静态性能的基础上，通过灵敏度分析对整车结构进行尺寸和形状优化，以实现结构的轻量化。阮景奎等^[3]针对汽车转向垂臂进行轻量化设计，以垂臂体积最小和极限工况下最大应力最小作为设计目标，先对其拓扑优化，而后对拓扑优化区域重新进行尺寸优化，取得了较好的轻量化结果。Kim^[4]选取汽车履带杆的6个变量（连杆厚度、连杆壁厚、纵肋数量、纵肋高度、纵肋厚度、横肋厚度），通过CAE分析研究履带杆刚度和强度随尺寸变化的规律；采用MatLab软件对试验设计的结果进行分析，选取影响最大的因素建立最优轻量化设计条件。Sookchanchai等^[5]针对汽车悬架下控制臂进行拓扑优化，以减轻重量和提高性能。

综上，围绕汽车零部件优化的轻量化设计已取得显著成果，但基本上以塑性材料作为优化目标，对铸造件产品，如汽车差速器壳体的轻量化较少提及。作为铸造件，差速器壳体的加工工艺以车、削、铣等尺寸加工为主，因此通过尺寸优化实现部件减重是最为便捷的方法；但需要注意壳体作为主要承力部件的应力分布变化情况。本文以某新能源乘用车的差速器壳体为研究对象，在起步和倒车时低转速、大扭矩的工况下，以壳体相关厚度尺寸作为设计变量，基于多目标遗传算法进行尺寸优化，以期同时实现壳体的轻量化和极限工况下最大应力的最小化。

1.   差速器壳体模态分析

1.1   有限元模型建立

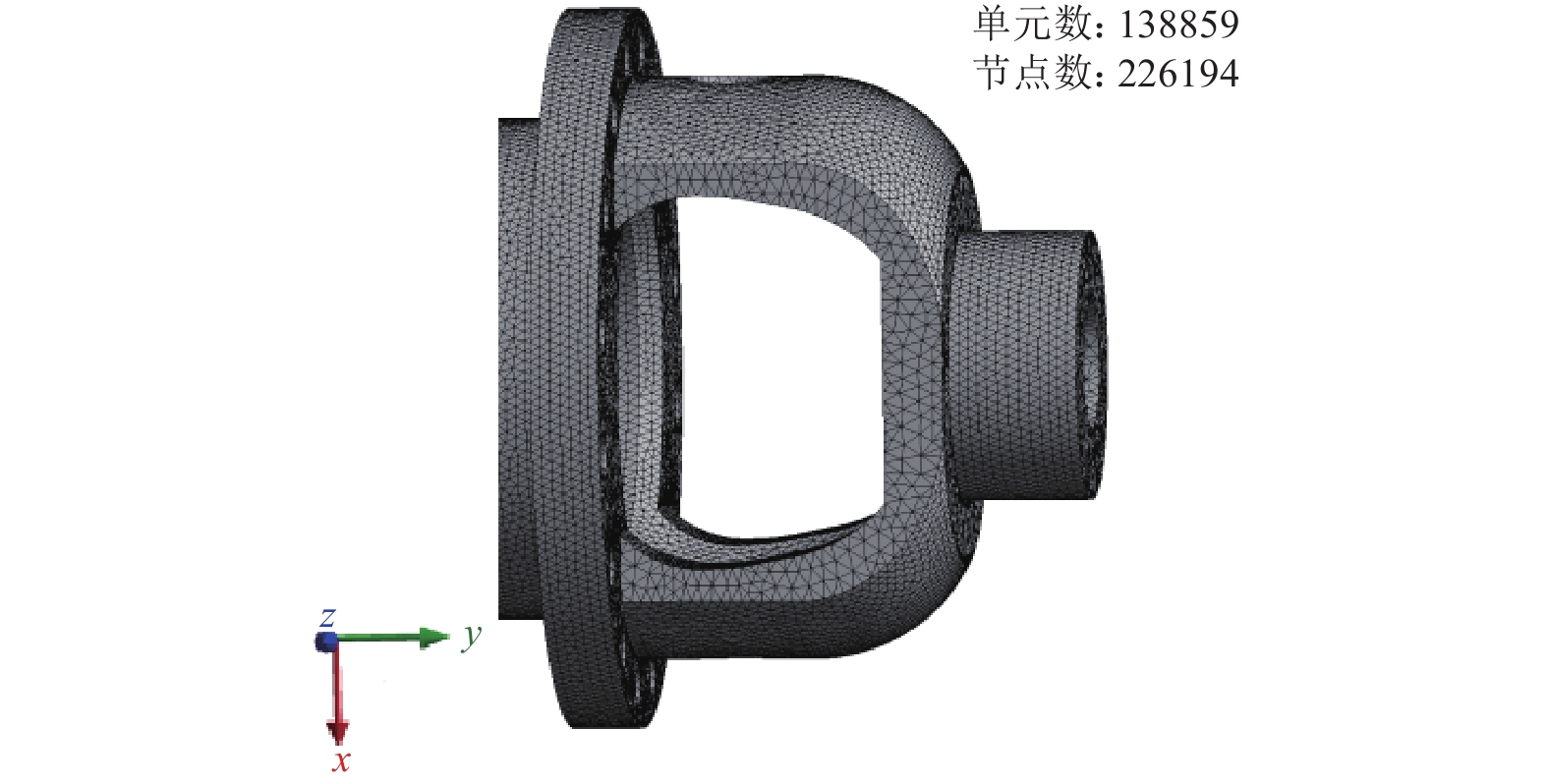
在导入有限元软件进行有限元模型求解之前，需要对差速器壳体的模型进行简化，以便划分高精度网格，减少软件运算量，降低产生错误解的概率。模型简化的原则为忽略对性能分析基本无影响的孔、倒角、圆角、小构件以及其他细节特征。本文涉及的差速器壳体材料为球墨铸铁（型号QT600-3），利用SolidWorks实体软件建立壳体参数化模型后，通过对应的接口打开ANSYS软件，赋予材料属性，得到差速器壳体的有限元模型如图1所示。

图  1  差速器壳体有限元模型

Figure  1.  Finite element model of the differential case

下载: 全尺寸图片 幻灯片

1.2   模态分析

依据该差速器壳体生产商提供的QT600-3材料相关属性，其密度为7.3×10³ kg∙m^-3，弹性模量为1.7×10¹¹ MPa，泊松比为0.3，屈服极限为370 MPa。模型网格划分使用二阶四面体单元，相较于一阶四面体网格，其精度更高、收敛速度更快；网格尺寸为2.5 mm，最终得到的差速器壳体网格模型如图2所示，共计138 859个单元、226 194个节点。

图  2  差速器壳体网格模型

Figure  2.  Mesh model of the differential case

下载: 全尺寸图片 幻灯片

模态可衡量结构系统的动态特性，是物体的固有属性。差速器壳体在传动系统中主要受到从动齿轮之间的啮合频率和转动频率影响，以及由于路面激励而引起的振动。

本文所研究的某新能源电动车额定转速为5000 r∙min^-1；主动齿轮齿数z₁为20，一档齿轮以及倒车档齿轮齿数z₂和z₃分别为45和52，从动齿轮齿数z₄为90。从动齿轮的转速为n，转动频率^[6]为

啮合频率^[6]为

由式(1)、式(2)可以求出该新能源电动车差速器从动齿轮的转动频率和啮合频率分别为18.5 Hz和1665 Hz。

考虑差速器壳体的固有振动特性由其低阶模态频率决定，结合差速器壳体实际运动工况计算其前4阶约束模态。在ANSYS中约束壳体两侧大端和小端圆柱面位置上的径向、切向、轴向位移，以及两处行星孔圆柱面上的轴向位移，通过迭代法求解出壳体前4阶模态的固有频率，如表1所示。

表  1  差速器壳体模态计算结果

Table  1.  Calculation results of the differential case modal

模态阶次	固有频率/Hz	振型
1	4 550.4	扭转
2	4 598.1	弯曲扭转
3	5 288.9	拉缩弯曲
4	5 308.7	弯曲

下载: 导出CSV 

| 显示表格

由表1可知，差速器壳体结构的一阶固有频率超过4500 Hz。比较此前计算的从动齿轮转动频率和啮合频率，同时考虑路面激励频率一般在50 Hz左右^[7]，可以排除壳体结构产生共振的可性。

2.   差速器壳体有限元分析

2.1   极限工况分析

相较于传统燃油车动力输出平顺的特点，以电能为动力驱动的新能源乘用车在起步和倒车时其传动系统的工况特点是低转速、大扭矩。而差速器作为动力输出端，其壳体承担了极限工况下的力作用。查阅文献[8]得知，差速器在电动机最大扭矩且一档传动时所受扭矩最大。因此，本文选定以下2种工况进行差速器壳体的静力学分析：

1）起步工况——电能驱动下电机最大扭矩输出且一档传动。

2）倒车工况——电能驱动下电机最大扭矩输出且倒档传动。

2.2   静力学分析

按照上述车辆行驶工况，同时以满足差速器壳体使用安全系数至少为1.2的要求进行轻量化设计^[9]。给定该新能源乘用车型的相关动力参数如表2所示，可计算得到：输入到差速器上的转矩在起步工况下为7 775.74 N∙m，在倒车工况下为6 918.43 N∙m。再由力学分析软件Romax Designer计算出2种工况下差速器壳体x、y、z方向的受力，如表3所示。

表  2  新能源乘用车的整车动力参数

Table  2.  The overall vehicle power parameters of new energy passenger vehicle

参数	数值
电动机额定转速Nmax/(r∙min-1)	5000
电动机最大扭矩Tmax/(N∙m)	300
一档传动比i1	3.501
倒挡传动比ir	3.115
主减速器传动比i0	7.793
传动效率ηT	0.95

下载: 导出CSV 

| 显示表格

表  3  极限工况下差速器壳体受力

Table  3.  Forces on the differential case under extreme conditions

工况	壳体受力/N
	x向	y向	z向
起步	-16 004	-65 480	50 840
倒车	28 886	58 764	59 928

下载: 导出CSV 

| 显示表格

按照1.2节中建立的差速器壳体约束条件，施加极限工况下的载荷，在WorkBench静力学模块中进行分析求解可知：壳体最大应力在起步工况下为203.85 MPa（见图3(a)），在倒车工况下为217.32 MPa（见图3(b)），均小于其材料屈服极限；壳体安全系数为1.7，大于最低使用安全系数1.2。因此，该结构具有充足的优化空间，可以进行轻量化设计。

图  3  差速器壳体静力学分析

Figure  3.  Static analysis of the differential case

下载: 全尺寸图片 幻灯片

3.   基于多目标遗传算法的差速器壳体优化设计

3.1   优化的约束条件及目标函数

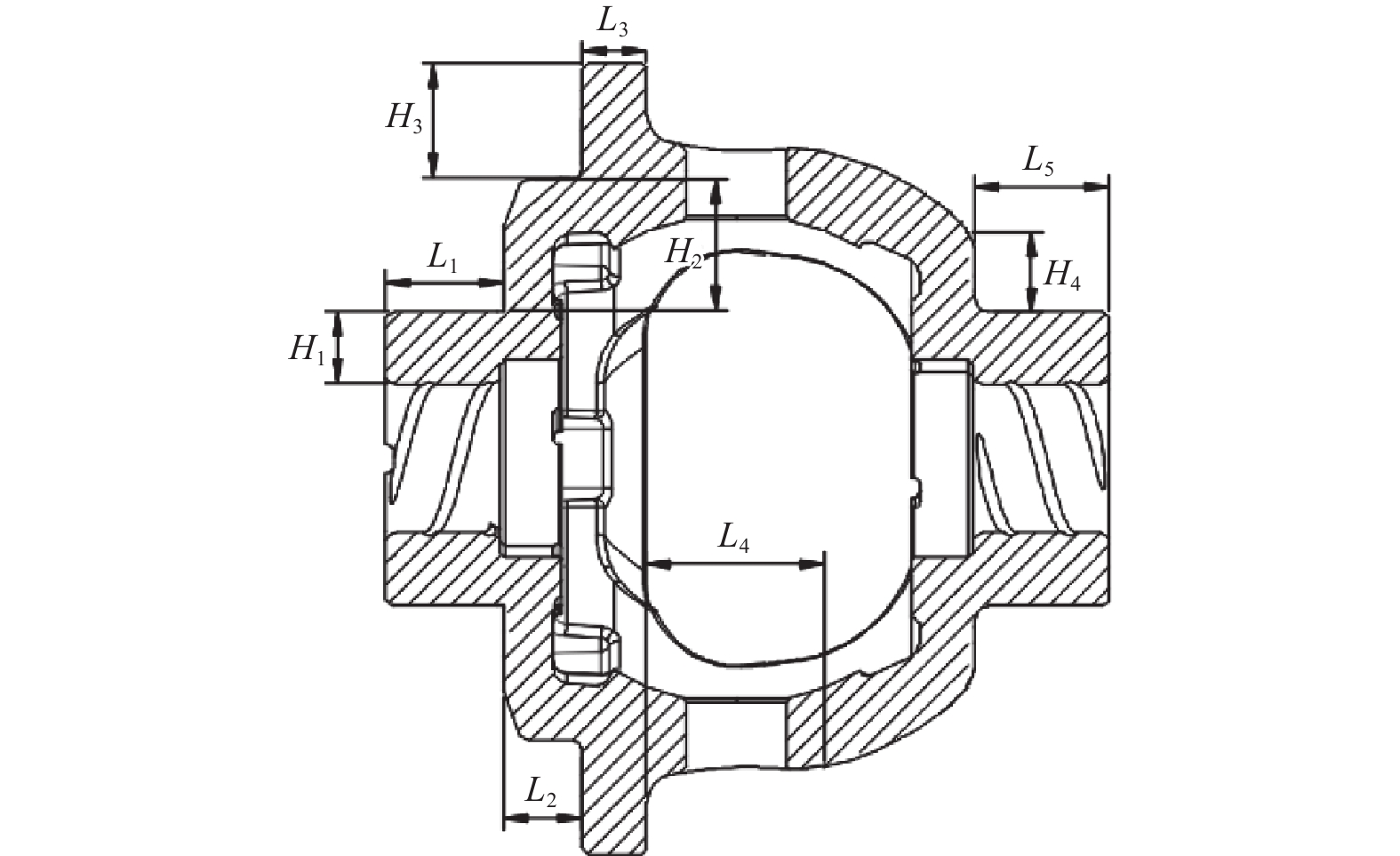
在SolidWorks中对差速器壳体的尺寸实施参数化驱动后，以模型中的参数化部位作为设计区域。为了有更好的优化结果，选取差速器壳体各个部位的厚度和长度作为设计变量，即：X=(x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉)=(H₁, L₁, H₂, L₂, H₃, L₃, L₄, L₅, H₄)，如图4所示。

图  4  差速器壳体设计变量

Figure  4.  Design variables of the differential case

下载: 全尺寸图片 幻灯片

可以看到，所有选定的设计变量均与壳体厚度、长度相关；而涉及差速器壳体装配的位置（如半轴孔、行星孔、法兰部位螺栓孔以及腔体内部内档、止口等部位）的尺寸参数、位置度及同轴度等均没有变化，不会影响装配，故不考虑。同时为避免参数化区域中某个尺寸过大的自由变形导致整体畸形，参考设计图纸，设置各设计变量的取值范围：15.3 mm≤x₁≤17.0 mm；24.85 mm≤x₂≤26.00 mm；28.25 mm≤x₃≤29.00 mm；16.3 mm≤x₄≤18.0 mm；24.0 mm≤x₅≤27.0 mm；14.4 mm≤x₆≤17.6 mm；36.8 mm≤x₇≤39.0 mm；27.0 mm≤x₈≤30.0 mm；14.4 mm≤x₉≤17.0 mm。

以差速器壳体总质量最小以及起步和倒车工况最大应力最小为优化目标，同时壳体结构的屈服强度和变形量均需满足安全标准下的极限屈服强度和极限变形量要求，建立多目标优化的数学模型

式中：m(x)为壳体质量，kg；σ(x)为极限工况下的最大应力，MPa；s(x)为极限工况下的变形量，mm；[σ]为材料的极限屈服强度，MPa；[S]为材料的极限变形量，mm；X_min和X_max分别为设计变量的下限值和上限值。

3.2   响应面分析

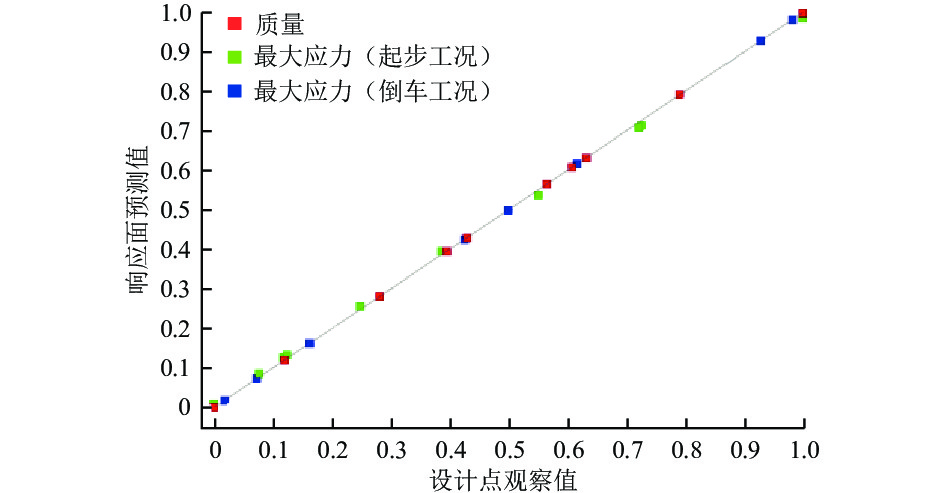
基于多目标遗传算法求解差速器壳体优化的Pareto解集之前，通过ANSYS软件中的实验设计（DOE）模块^[10]，根据设计变量的可行域，采用最佳空间填充设计法进行实验设计，以构建一个准确的响应面来拟合设计变量同目标函数之间的隐式关系。完成响应面分析后，得到各试验设计点的离散图如图5所示。可以看出，质量、起步工况最大应力以及倒车工况最大应力三者都十分靠近对角线位置，反映出它们与设计变量的拟合程度较高^[11]。相反，如果试验设计点较为离散，拟合程度差，说明设计变量与目标函数之间存在错误关系，此类优化问题无法得出正确的解。

图  5  响应面拟合离散图

Figure  5.  Fitting discrete graph of response surface

下载: 全尺寸图片 幻灯片

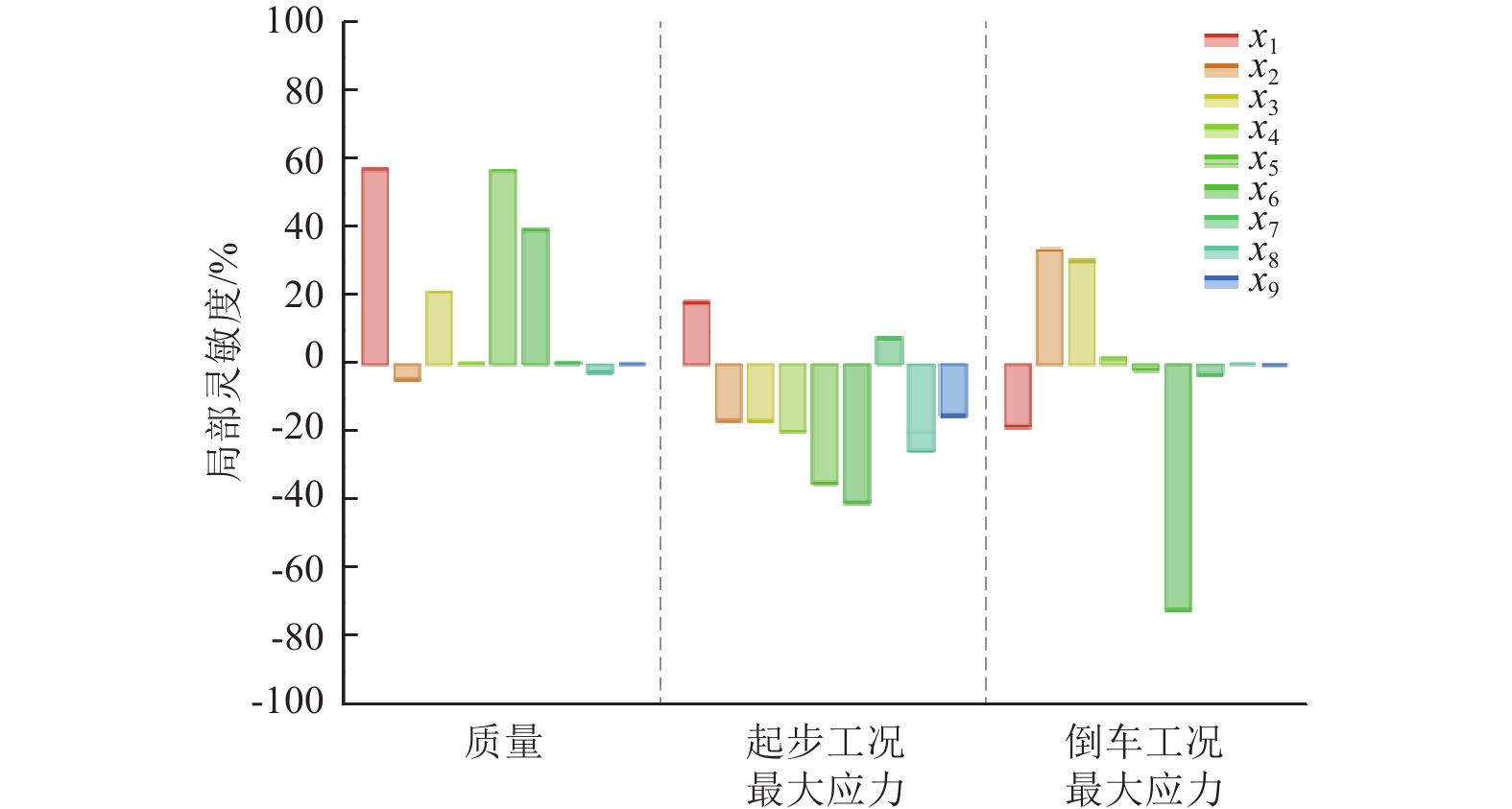
通过响应面分析得到各设计变量对质量和极限工况下最大应力的局部灵敏度如图6所示，它反映了输入参数对输出参数的影响。显见，差速器壳体上大端厚度x₁、法兰后外廓高度x₃及法兰厚度x₆等设计变量对于质量的灵敏度呈现正相关性，但是对最大应力的灵敏度呈现负相关性，说明质量与最大应力这两个目标相互矛盾。鉴于此，需通过多目标遗传算法的优化，在保证轻量化的前提下，得到符合结构应力最小的设计变量解。

图  6  设计参数的局部灵敏度

Figure  6.  Local sensitivity of design parameters

下载: 全尺寸图片 幻灯片

3.3   算法求解

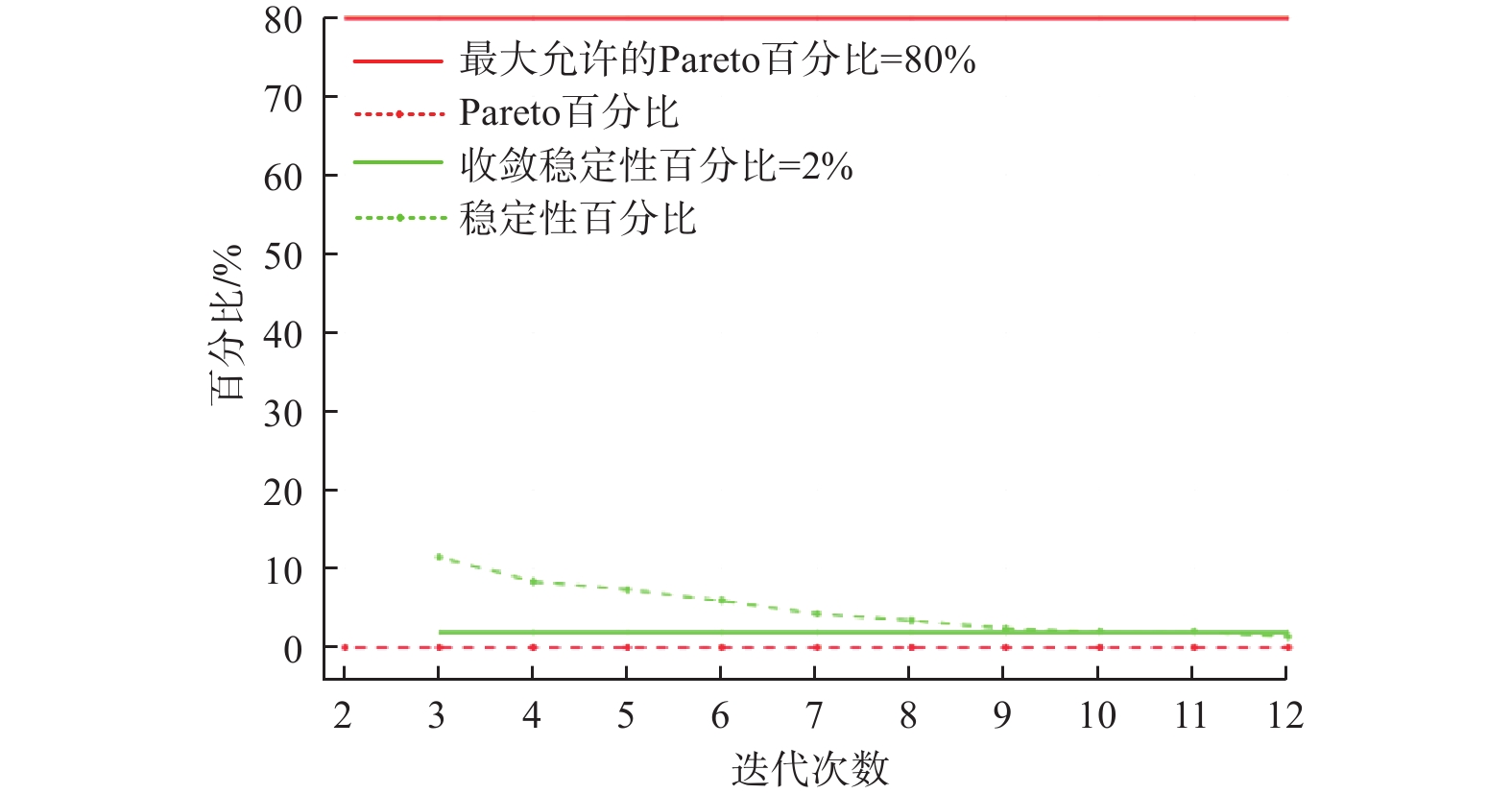
多目标遗传算法NSGA-Ⅱ不仅能够降低计算的复杂度，提高精度，还能够保证Pareto解集的多样性，很适合全局领域的最大、最小值的多目标求解问题。根据3.1节建立的多目标优化模型，设置初始种群数3000个，交叉概率为0.8，迭代次数为40，最大候选点个数为3。通过ANSYS软件优化求解，经过40次迭代计算，或当80%的样本数布落在Pareto前沿时迭代完成。根据图7所示的迭代过程可以看出，此次迭代在稳定性低于2%时趋于收敛，在12次优化迭代后达到收敛。

图  7  目标函数的迭代过程

Figure  7.  Iterative process of objective function

下载: 全尺寸图片 幻灯片

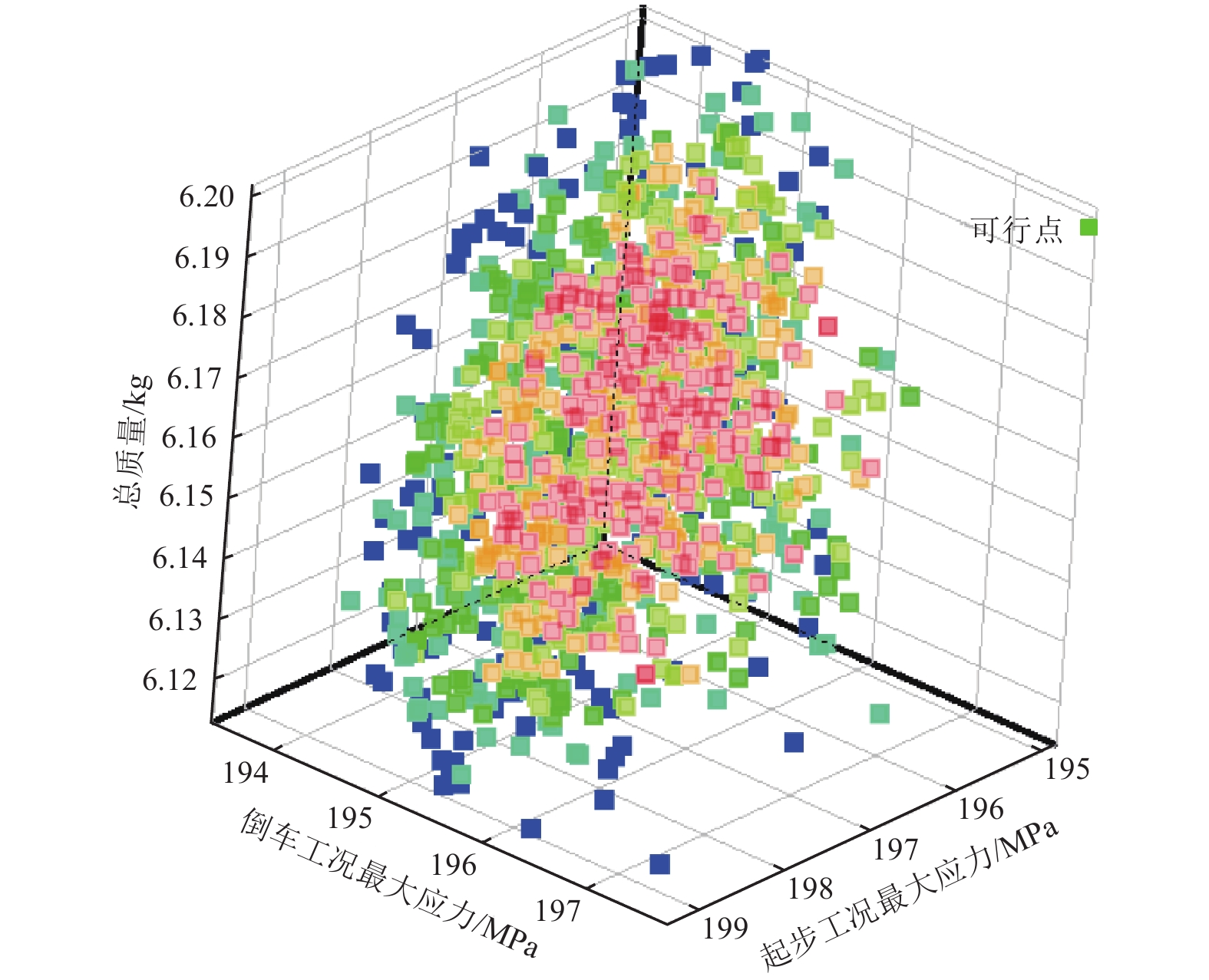
最终求解得到1组差速器壳体的Pareto解集，如图8所示；此外，系统根据最大候选点数，提供了3组优化方案，其中任意1组都可作为确定结果，在选定其一之后与初始结构参数的对比如表4所示。表中还包含根据差速器壳体的车、铣加工工艺要求，以及对设计变量优化值进行圆整的取值。

图  8  差速器壳体Pareto解集

Figure  8.  Pareto solution set of the differential case

下载: 全尺寸图片 幻灯片

表  4  差速器壳体设计变量优化结果对比

Table  4.  Comparison of optimization results of design variables of the differential case

单位：mm
设计变量	x1	x2	x3	x4	x5	x6	x7	x8	x9
优化前	17.25	26.00	28.50	18.00	27.00	16.00	37.80	30.00	16.00
优化方案1	15.624	25.354	28.314	17.125	24.762	17.281	38.61	29.685	16.237
优化方案2	15.636	25.424	28.312	17.164	24.725	17.264	38.586	29.751	16.417
目标方案	15.353	25.232	28.265	17.667	25.119	16.822	38.435	29.684	16.286
圆整值	15.35	25.23	28.27	17.67	25.12	16.83	38.44	29.68	16.29

下载: 导出CSV 

| 显示表格

3.4   工艺尺寸链分析

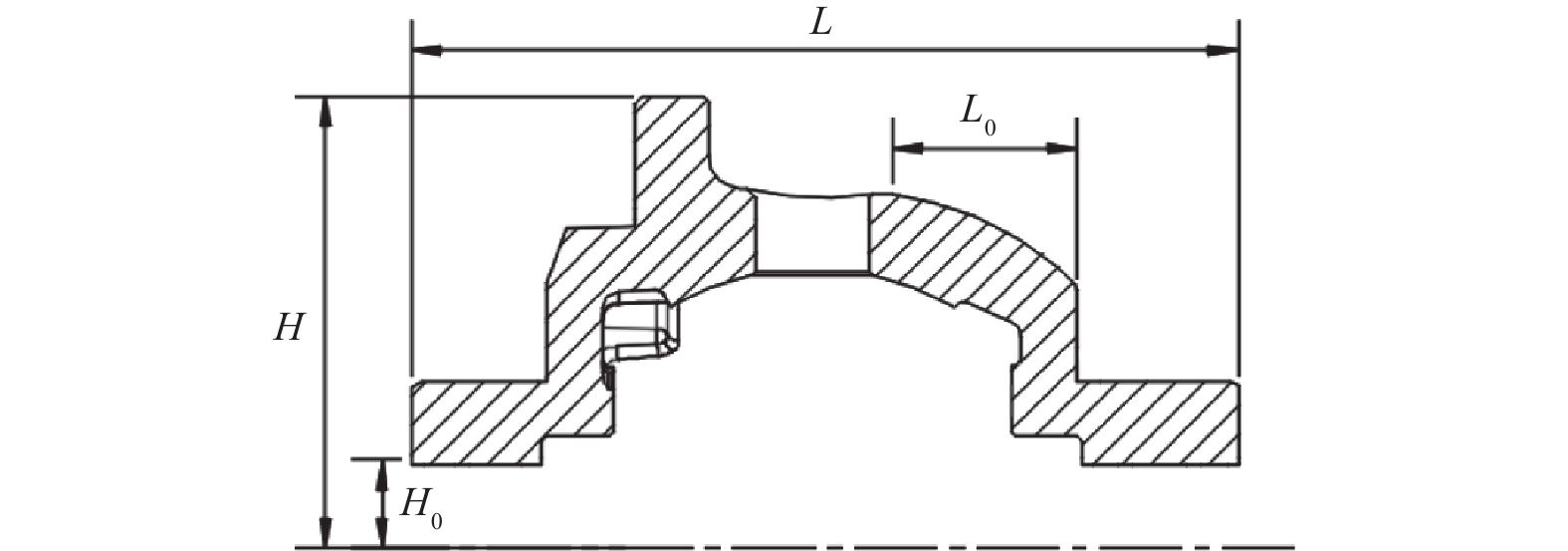
如前所述，所选的壁厚设计变量均是在不影响装配情况下进行优化的，为进一步保证壳体在后续机加工工艺中参照给定的优化工艺参数加工后不会出现壁厚差异过大而导致结构强度变化，对壳体轴向零件尺寸链以及径向装配尺寸链进行分析。如图9所示：差速器壳体零件图纸给定其轴向尺寸总长L为(157.1±0.1) mm，径向尺寸H为(84.24±0.1) mm，壳体上半轴孔直径为31 mm，弧面水平方向尺寸为29.25 mm。根据封闭环基本尺寸等于所有增环尺寸之和减去所有减环尺寸之和可知，参照图4，径向封闭环尺寸为

图  9  差速器壳体尺寸链分析

Figure  9.  Dimensional chain analysis of the differential case

下载: 全尺寸图片 幻灯片

轴向封闭环尺寸为

根据优化后的圆整值求得：H₀=(15.5±0.1) mm，L₀=(29.25±0.1) mm。根据结果可知，径向和轴向封闭环的尺寸分别吻合径向装配尺寸链以及壳体轴向零件尺寸链，这也是壳体参数化设计时约束了整体径向和轴向尺寸的结果——通过尺寸链分析得到了设计变量优化值的关联性和可靠性，保证了机加工时厚度的均匀性。

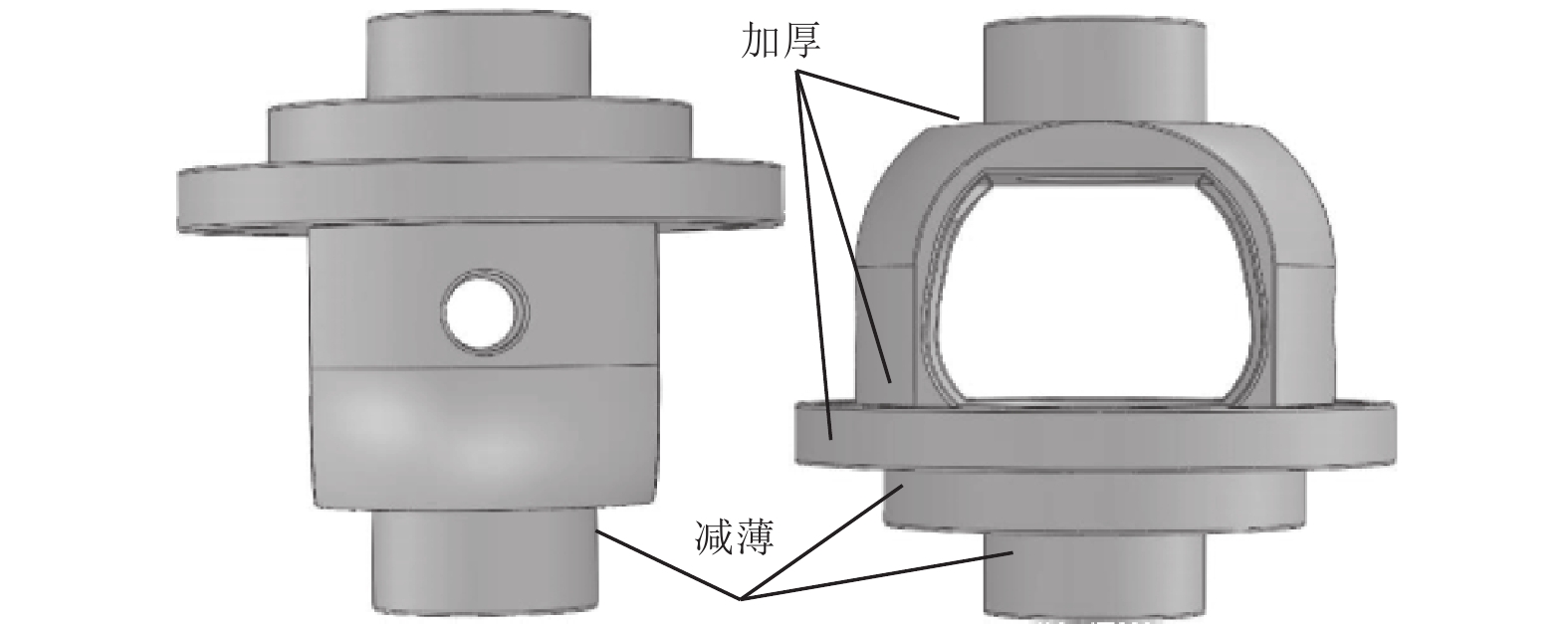
进而建立优化后的差速器壳体三维模型，如图10所示。相比于优化前模型，轻量化模型的变化集中在大、小端以及腔体根部尺寸的减小，但对法兰部位以及腔体外部和肩部应力过大的地方增加材料进行了加固。壳体的整体质量由6.80 kg减为6.10 kg，减少了10.3%

图  10  优化后的差速器壳体模型

Figure  10.  Optimized model of the differential case

下载: 全尺寸图片 幻灯片

4.   优化结果验证对比

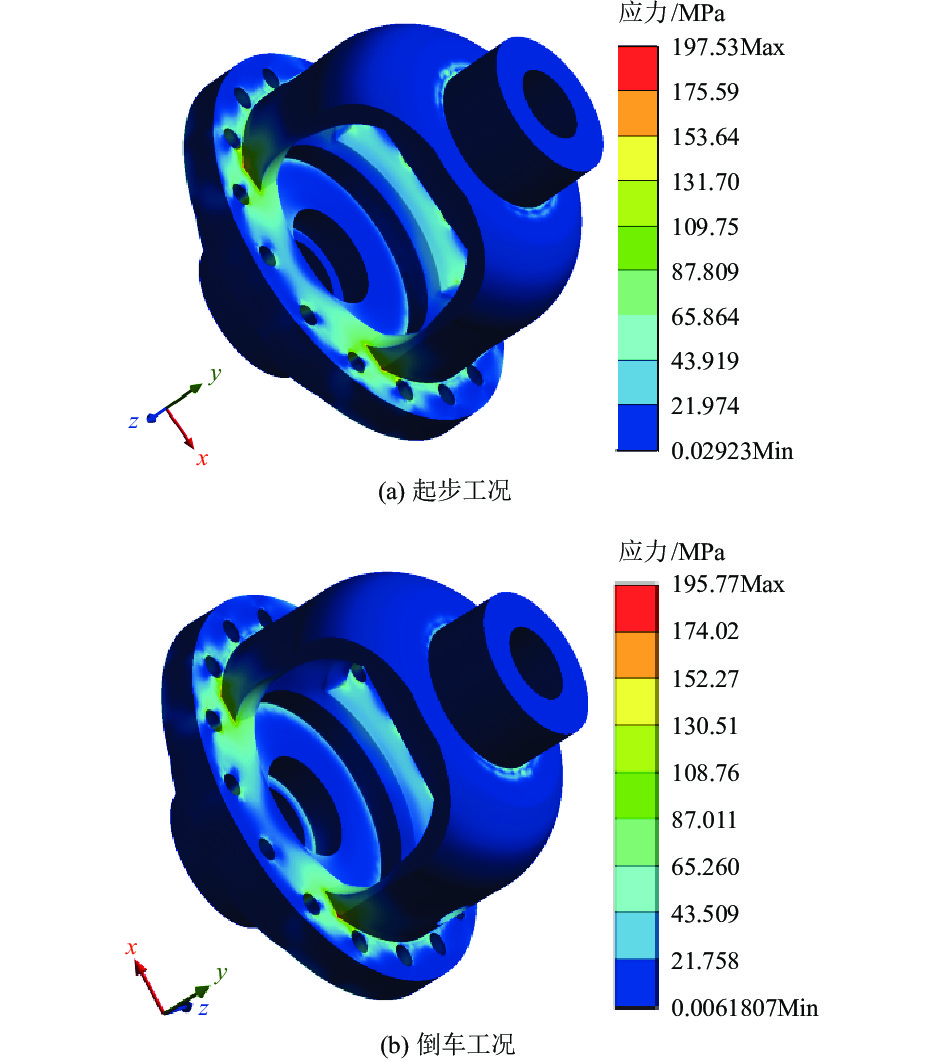
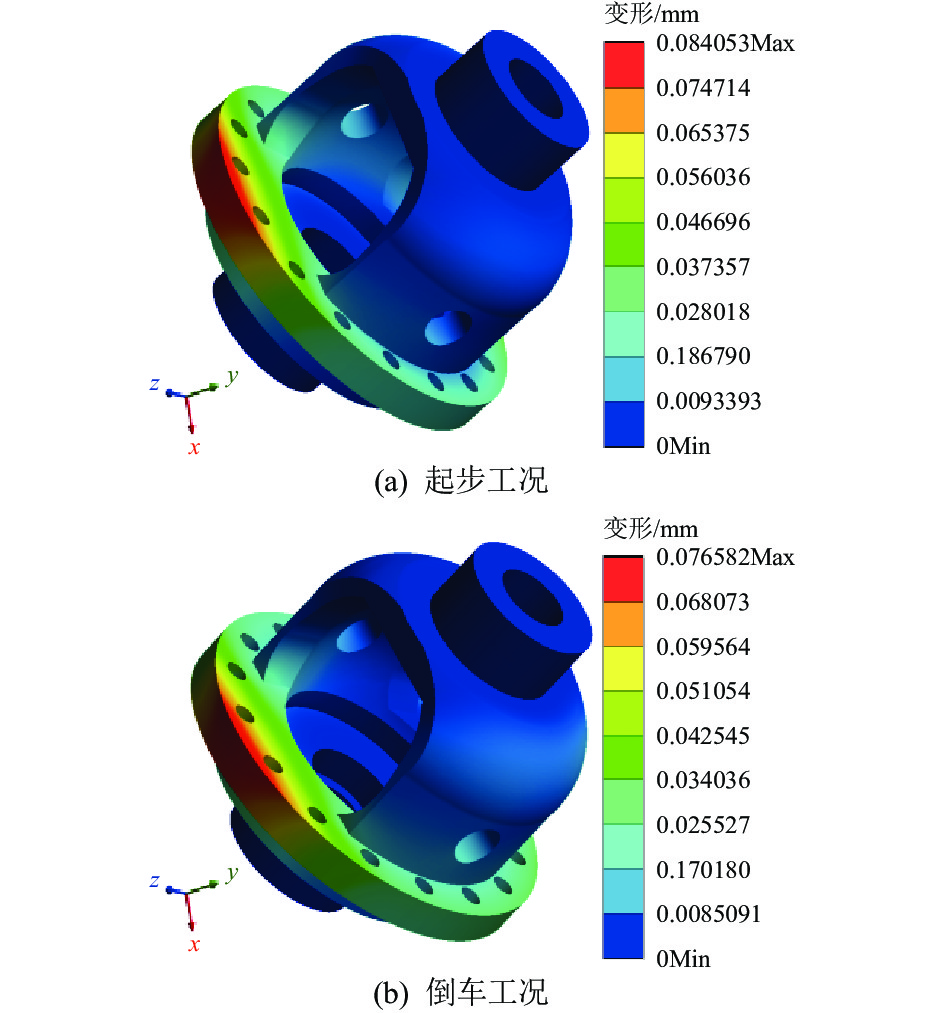
通过ANSYS软件，在同样的载荷和边界条件下，对优化后的差速器壳体模型进行静力学分析，得到其应力和变形云图如图11和图12所示。

图  11  优化后的差速器壳体应力云图

Figure  11.  Stress nephogram of the optimized differential case

下载: 全尺寸图片 幻灯片

图  12  优化后的差速器壳体变形云图

Figure  12.  Deformation nephogram of the optimized differential case

下载: 全尺寸图片 幻灯片

由图11(a)可知，在起步工况下，优化后模型的最大应力为197.53 MPa，比优化前模型的最大应力203.85 MPa减小了6.32 MPa。由图11(b)知，在倒车工况下，优化后模型的最大应力为195.77 MPa，比优化前模型的最大应力217.32 MPa减少了21.55 MPa。最终，轻量化后的差速器壳体最大应力降低了9.9%，结构安全系数为1.87（＞1.2），满足强度要求。

由图12(a)可知，优化后模型的最大变形为0.084 mm，根据QT600-3的材料延伸率δ≥3%，可知该最大变形量满足材料安全应用要求。

同时，通过应力云图可以看出，除应力集中位置外，优化后的差速器壳体在不同位置上无较大强度差异。

5.   结束语

本文首先通过ANSYS软件计算差速器壳体有限元模型前4阶模态的固有频率和静力学分析，证明差速器壳体具备轻量化的设计空间；然后建立差速器壳体的多目标优化数学模型，并通过最佳空间填充实验设计法得到目标函数的响应面拟合度以及目标函数对设计变量的局部灵敏度；最终基于多目标遗传算法的优化求解，参考Pareto最优解集，轻量化后的差速器壳体整体质量减少了10.3%，最大应力降低了9.9%，最大变形在安全范围内，证明通过多目标遗传算法进行轻量化设计是可行的。本研究可为航天器部件结构的轻量化设计提供参考。